06 de agosto de 2025
TCC - Bacharelado em Física










































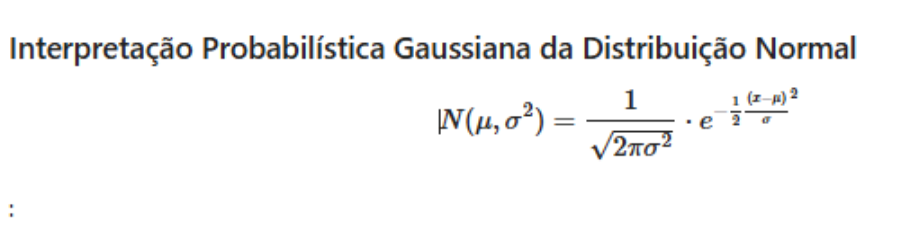




Da página 02 à 06
Da página 07 à 12
Da página 13 à 17
Da página 18 à 23
Samuel Delmonte

O Blog do Pensamento Libertário.

Samuel Delmonte
< ⁄ > All application developed with pure code.
Uma breve exposição acadêmica e profissional...
Algumas publicações no meu Canal do YouTube...
Uma vinheta introdutória do meu trabalho...
Acesse Aqui
b ∫ a b f(x)dx = b lim n → ∞ n ∑ i=1 b (b-a) n b f(xi)
Você pode assistir os vídeos do Curso de Cálculo - Isto é só para loucos aqui mesmo, ou na plataforma do YouTube:
Punk's Not Dead!
Você pode assistir os vídeos da Playlist sobre o Punk aqui mesmo, ou na plataforma do YouTube:
My Eight Favorite Authors
Você pode assistir o vídeo OS 8 autores que me formaram aqui mesmo, ou na plataforma do YouTube:
Muller, o jogador.
Você pode assistir os vídeos sobre os gols e as habilidades do ex-jogador Muller aqui mesmo, ou na plataforma do YouTube:
O conteúdo deste blog não se resume à abordagem de apenas um assunto, mas sim vários deles; na verdade, o assunto em si, pouco importa, sendo, pois, relevante a origem da opinião a respeito deles. Esta obra apresenta o estilo baseado em aforismos, independentes entre si, no entanto, todos eles, são oriundos do livre pensar, da mesma métrica cognitiva, sendo este pensamento denotado como, o Pensamento Anarquista, sem dogmas preestabelecidos. Embora esta obra, tenha vínculo com o pessimismo, e repudie os arcaicos dogmas morais, ela também tem suas bases edificadas em grandes pensadores; não exatamente com suas ideias creditadas integralmente, mas sim nas parcialidades das quais o autor assimila como verdades, completadas com as suas próprias convicções sobre elas (as verdades). Portanto, as linhas que, daqui em diante seguirão, buscam desconstruir os valores morais, ditos universais e laureados como Leis inalteráveis. Para isso, a liberdade de pensamento deve ser soberana, cujos limites são corajosos o bastante para, superar dogmas morais pré-estabelecidos; este Pensamento Libertário, de coragem, inspira-se na Anarquia...!!!
06 de agosto de 2025





























































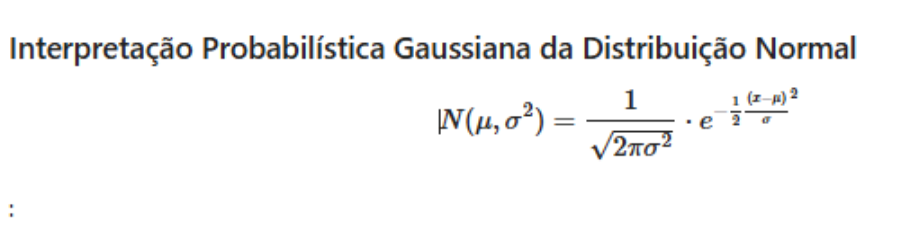









Da página 02 à 06
Da página 07 à 12
Da página 13 à 17
Da página 18 à 23
Samuel Delmonte
16 de janeiro de 2025
Erwin Schrodinger, foi um físico austríaco, formulador,no ano de 1926, da equação que, além de carregar consigo, seu nome, constituiu a base formal teórica da mecânica quântica. No entanto, novos desdobramentos a respeito de certas premissas da teoria quântica, fizeram-o, assim afirmar:
- Não gosto disto, e lamento ter contribuído para isto!
Ele morreu convencido de que, o arcabouço teórico da física quântica, cujo legado pessoal estava incluido, era inverossímil frente a realidade. A equação de Schrodinger continua válida.
$x_{n}=x_{0}+n\Delta x$, com $\Delta x =\frac{(x_{N}-x_{0})}{N}$ :
Samuel Delmonte
15 de janeiro de 2025
Sobre a natureza quantica das medições e observações, ele perguntou:
- Acreditam, realmente, que a Lua somente existe quando olhamos para ela?
$$resultando:$$
Samuel Delmonte
27 de agosto de 2024
Pergaminho bíblico, de aproximadamente dois mil anos, encontrado, em 2021, na Judéia, atual Cisjordânia:
Quando ele se aproxima, os montes tremem e as colinas se derretem. A terra treme na sua presença; sim,
mundo e todos os que nele vivem. Quem pode resistir à sua indignação? Quem pode suportar o despertar da
sua ira? O seu furor se derrama como fogo, e as rochas se despedaçam diante dele.
Alude-se ao Rei Davi (séc. XI ac – séc. X ac), tal qual transcreve a bíblia judaica, a alcunha [..] dum homem segundo o
coração de deus [..]; e mais, muito mais do que isso, a Davi , o mais conhecido dos reis judeus da antiguidade,
imputa-se o status de - ser o preferido Dele -, dado que, arrependia-se dos seus pecados, diante de Yahweh.
Davi, simboliza ao judaísmo, o ideal do judeu que, por Ele, foi escolhido, visto que, (o Rei Davi), integra a
linhagem genealógica semita primordial, cujo início se dá com Abraão, e seus sucessores vão de reis a profetas,
manifestando, nas suas menções bíblicas, grosso modo, a aliança estabelecida pelo povo escolhido com seu deus,Yahweh.
Qualquer outra dinastia, cuja procedência seja próxima aos primordiais, citados acima, usufruirá de prestígio,
notoriedade e, o mais importante, atingirá longevidade secular, de suas memorias, transmitidas às gerações futuras.
Ao ser-lhes atribuída semelhante adjacência, os Abravanel, tornaram-se detentores de robusta importância no contexto
da história judaica, além de vasta documentação nas literaturas disponíveis. Entretanto, antes de aprofundar nesta
antiga história:
-É-me indispensável esclarecer, a respeito da escassez de fundamentação cientifica, que corrobore a validade dos
eventos, aqui abstraídos, de tal modo que períodos anteriores ao Renascimento (séc. XI ac - séc. XIII),
minguam em indícios que legitimem relações familiares de longas arvores genealógicas; ademais,
grandes personagens dos contos bíblicos, sequer possuem qualquer rastro de que, algum dia existiram,
tais comoAbraão, Moisés e outros; quanto a Davi, há algo de indícios a seu respeito, mas sem as
alegorias que saturam os textos bíblicos.
Contudo, em meados do século XV, instaura-se o período moderno (Idade Moderna, convencionada
entre os anos de 1453 – 1789 ), cujo marco inicial, se dá com a queda do Império Romano do Oriente (Bizantino),
por meio da retomada de Constantinopla, pelos turcos, emergindo, deste modo, um novo status quo,
[…] o Império Otomano.
Embora, seja notório, o evento, acima relatado, pode-se concluir que, a chegada dos novos tempos acontece quando o
século XV, torna-se testemunha da erradicação do feudalismo, e doutro modo, a aparição de estados absolutistas,
sedentos para serem financiados pela nova modalidade econômica, instaurada pelas expansões marítimas, que
constroem, pouco a pouco, o Mercantilismo, o embrião do modelo Capitalista.
É nesse contexto, que ilustres integrantes da burguesia, assumiram posição de destaque, tal qual o fizeram os
integrantes da família Abravanel, que deste ponto adiante, conquistam notoriedade, afinal despontaram como
exímios estadistas, filósofos, comerciantes, financiadores, contadores, entre outros. Indivíduos
tais como Judá Abravanel (Tesoureiro – Espanha ~ 1310), Don Isaac Abravanel
(Estadista, filósofo – Lisboa – 1437-1508), Samuel Abravanel (Estadista, financiador – Lisboa – 1473-1551),
etc., galgaram significante importância na construção do mundo moderno.
Os Abravanel, foram impulsionadores do Mercantilismo, tanto na Espanha como em Portugal, financiaram navegações,
tal como a de Cristóvão Colombo, em 1492. Entre os séculos XV e XVI, ambos os países ibéricos,
simplesmente, possuíam até então, as maiores economias do mundo, com boas perspectivas de, assim manter-se;
eles (os Abravanel), muito contribuíram para tal.
Foi então que, portugueses e espanhóis decidiram que era hora de reformar, e desbravar novas Cruzadas, recorrer
aos autos da fé, por meio da Inquisição, administrada por Tomás de Torquemada
(Inquisidor-Geral – Espanha – 1420 - 1498),
com plenos poderes sobre os julgamentos inquisitoriais. Ademais, foram decretadas, entre a última década do
século XV e a primeira do século XVI , as expulsões dos judeus da Espanha e de Portugal, levando consigo,
os conhecimentos mercantis.
Dá-se início uma nova diáspora, e assim como muitos judeus, os Abravanel se dispersam pela Europa, África e América.
É desse acontecimento histórico, que eu, um torpe pesquisador da genealogia de minha família, com muitas dificuldades,
detectei indícios, que corroboram com a presença da minha família ancestral, nos grupos que perambulavam fugindo
das perseguições, e, tinham também, como integrantes alguns membros do clã Abravanel.
Porquanto, há prenúncios de que os Delmonte (meus antepassados), estabeleceram-se em Módena, na Itália,
no início do século XVIII, após peregrinarem pela Europa, na companhia dos Abravanel.
Enrobustece o fato deles, meus ascendentes, terem imigrado da Módena, do até então, Reino da Itália
, para o Brasil, em 1895.
Senor Abravanel (o Silvio Santos), não foi menos notável do que seus famosos antepassados, longe disso, ele demonstrou lealdade às suas raízes do começo ao fim, do camelô da juventude, ao banqueiro da maturidade, manifestou o quão importante era, para ele, transmitir sua tradição familiar adiante, perpetuando, de certa forma, aqueles que já não estão. Parece que, ele atribuía ao conjunto de características genéticas hereditárias, o sucesso de suas empreitadas, durante a vida. Era seu segredo!
Ele, o Silvio Santos, viveu, de fato, como um notório Abravanel, até o fim.
À semelhança de Senor Abravanel , que orientou familiares a conduzir seus ritos fúnebres, de acordo com a tradição
judaica, assim, também o fez, meu pai; inclusive, ambos estão no mesmo cemitério, além do meu primo-irmão Pedro.
Samuel Delmonte
03 de dezembro de 2023
[...] Este mesmo segundo desapareceu para sempre, perdeu-se na massa anónima do irrevogável. nunca mais regressará. Sofro e não sofro com isso. Tudo é único e insignificante[...]
De ano a ano, de revés em revés, mantenho-me surpreendentemente, vivo.
Assim como o grande filosofo do martelo (Nietsche) disse certa vez
[..] aquilo ou aqueles que não me
matam, tornam-me mais forte [...]
, representa fielmente a vida que levei e ainda levo.
Sei muito bem, que estou condenado a viver longevos anos, sentença, cuja imposição, permitirá enterrar a muitos que conheci.
É evidente, de acordo com o que expus acima, que sou cético e não acredito no ser humano.
Aliás existem inúmeros parasitas que buscam se relacionar com outras pessoas através do dinheiro; sobre esses desprezíveis seres, nada senão asco, posso sentir.
Apesar de todas as dificuldade e punições que recebi, e ainda recebo, da vida, não reclamo de nada, afinal foram todas consequências dos meus atos.
Não nasci com o dom da fé, portanto não acredito em destino algum, nem para mim, nem para os outros, de modo que estamos mais sozinhos do que imaginamos, entregues à própria sorte, numa aterrorizante realidade, cuja natureza, nas suas manifestações, sejam elas quais forem, é implacavelmente indiferente a todos nós. Ela (a natureza), não dita, tampouco supervisiona, quaisquer caminhos ou destinos, frutos de um sentido preestabelecido, existente antes mesmo, do início da jornada [...]
de tal modo que [..]
não há o que temer [...]
pois [...] não haverá salvação nenhuma, a ninguém.
Kafka, que das profecias citadas acima, é o maior dos profetas, define brilhantemente nossas
falsas aspirações a respeito da existência,
quando afirma que
[...] Esperança há muita por aí, mas não para nós [...]
. Resta-nos é claro, entorpecermos com triviais mentiras, tais como a existência absurda dum deus redentor.
A mim, crenças espirituais, não querem dizer nada; em contrapartida não há nada mais sublime do que tentar entender, mesmo que infimamente, as leis da natureza através das suas belas equações. Estas últimas sim, dizem-me muito.
Não existe motivo algum para estarmos aqui; somos apenas uma parte integrante da natureza que sintetizou moléculas,
a base de carbono, que desenvolveram a capacidade de criar cópias de si próprio; essa é a definição mais completa
dum ser vivo que já pesquisei, e a li no primoroso O Gene Egoísta (DAWKINS, 1976), de Richard Dawkins .
É, a meu ver, aquele que mais se aproximou do entendimento e razoes de existência, ou não, de seres portadores
da vida, após a monumental publicação de A Origem das Espécies (DARWIN, 1859), feita por
Charles Darwin.
Inevitavelmente, precisamos dar sentido às nossas breves existências, e para isso almejamos objetivos e nos esforçamos para concretizá-los.
Sem mais o que dizer, concluo ciente que sou uma das ovelhas que se perdeu, e conduzo a minha vida rumo a lugar nenhum.
Samuel Delmonte
02 de dezembro de 2023
Olá, meu querido pai...
Não se preocupe, afinal os laços que nos unem são maiores e mais fortes do que aqueles que nos afastariam.
Embora pensássemos que nossa origem fosse sefardita, ela é, na verdade, ashkenazita, assim como nossa rebeldia.
Portanto farei diferente...
Nesse próximo ano, não te pedirei perdão no “yom kippur” (dia do perdão), pois já é tarde para isso.
De modo que de hoje até o dia do perdão, carregarei contigo o amargo sabor das tuas lagrimas, resultantes da úlcera do arrependimento.
Enquanto viver, farei o que for possível para que sua netinha saiba quem algum dia você foi.
Após isso, rogarei para ser levado aos jardins do pecador...
Rogarei, também, para ser enterrado e finalmente descansar em paz, afinal você e eu sabemos bem que a hora da verdade chegará para todos e ninguém sairá vitorioso, pois, iniciar-se-á a inexistência.
Como esse dia já te alcançou, meu pai, descanse...
Samuel Delmonte
08 de novembro de 2023
"Nos dias de hoje, apenas nos ateus sobrevive a paixão pelo divino. Nenhum outro se salvará.
Certa vez, sai de casa em busca do sentido que os outros dão à vida; e, por mais que, exaustivamente o procure, fi-lo em vão, pois não há na natureza, eventos de essência a priori, específicos aos seres humanos; há, em contrapartida, implacáveis indiferença e aleatoriedade flutuando entre nós. Existe, para todos, uma derrota anunciada, no final das contas. Nenhuma salvação nos acometerá!
Perambulam, por toda parte, fabulas emergidas do devaneio humano, capazes de encenar um roteiro da realidade, alicerçado na existência de um sentido preestabelecido, que por sua vez, molda um destino quase linear, rumo à redenção futura.
Grosso modo, é desta última etapa, que a embriagues de todo o processo, deseja desembocar. Deste modo, soluciona-se os dois grandes pavores da humanidade ,desde sempre: conquistar a vida eterna, como resultado da vitória sobre a morte biológica, e, o reencontro com os entes queridos que já não estão. Louco e brutal efeito placebo, que não aparenta haver cura.
Søren Kierkegaard, filosofo dinamarquês que, em meados do século XIX, afirmou serem fruto do desespero e angústia humanos, as
tentativas de conceber a natureza do indivíduo, passível em atingir a cristandade, status cujos atributos, supostamente, emanam da figura
e dos ensinamentos do judeu nazareno, Jesus Cristo. De tal modo que, esse conjunto de traços, ou melhor, a moral cristã exista a priori, desde sempre,
não como uma criação humana, mas sim preestabelecida antes da experiencia. A Kierkegaard, pareceu-lhe inverossímil tais relações; ironicamente, ele assim concluiu,
durante sua preparação para, tal qual seu pai, tornar-se pastor luterano.
O que a observação das experiencias nos mostra, é que o homem, com seus triviais defeitos de caráter, jamais se comporta como um altruísta,
durante a jornada do seu destino; tampouco, como um comunitário, transbordando em benevolências, ao invés disso, busca desesperadamente,
aliviar seu desespero humano, atribuindo a fatores externos, a esperança da qual jamais encontrará.
Diante disso, o que fazer durante a vida, curta, sofrida, ingrata; como perpetuar, aquilo que já não existe, ou, no seu devido tempo deixará de existir?
Schopenhauer dizia que entrava em contato com autores de séculos passados, quando estava com seus livros, neste momento, estes autores estavam com ele
Einstein disse que suas equações ficarão para a eternidade.
Percebe-se, em ambas as citações, que há a preponderância de significação de suas existências, regidas pelos respectivos recursos heterogêneos e individuais, aptos à apropriação durante o curso da vida e de acontecimento real periódico. Em vista disso, já não mais é necessário expectar uma redenção futura, pois, deixa-se de temer o invariável fim, onde nada mais acontecerá, e ao invés disso, possuir a coragem necessária para estar ciente da vulnerabilidade humana e que, em breve, se deparará com o dia da verdade, quando, inicia-se a inexistência.
Contudo, é notável a hegemonia da estupidez humana em criar roteiros encenados no pós morte, como por exemplo, o mercado de congelação da cabeça ou corpo inteiro de um cadáver, que em vida, convenceu-se de que poderia, um dia, ser ressuscitado.
Sem mais argumentos, encerra-se aqui, este ensaio, citando a opinião de um eminente médico legista, quando questionado a respeito do congelamento de pessoas mortas.
-Carlos Delmonte-
Samuel Delmonte
18 de outubro de 2023
"Estar sozinho é treinarmo-nos para a morte."
Olá, amigos, inimigos e aspirantes, a ambos...
...eu ainda estou vivo, retornando do paraíso, cujo lugar, já frequentei inúmeras vezes e,
todas, eu disse todas as vezes que por lá estive, li ao adentrar, certa frase cravada na
sua porta, que aliás, são os mesmos dizeres concebidos por Dante Alighieri
, na sua Divina
Comédia (ALIGHIERI, 1321), assim ditos:
-Também a mim criou o eterno Amor.
Nesta minha última passagem pelo Paraíso, contemplei um debate em busca da liberdade entre os
animais que ali, também estavam. As lebres exigiam igualdade de direitos entre todos os
animais que conviviam nas colinas de Javé, o Deus Punitivo, no entanto, os leões, que
também lá estavam, disseram às lebres que para tal logro (a igualdade), deveriam lutar
com unhas e dentes.
Percebi agora, que vislumbro, desde aqui, o instinto primordial do ser vivo, a
razão pela qual a vida se perpetuou, oh louvável assombro! É do egoísmo que emana
a vida, grosso modo, parece haver uma condição necessária para criar copias de si próprio,
fenômeno que tipifica um ser vivo, tal incumbência se manifesta por meio de um ímpeto
individualista, atributo cujo proposito, determina que todas as ações de um indivíduo,
tem por fim, seu benefício próprio, sempre.
Conclui-se que Max Stirner havia acertado essa hipótese, exposta no seu O Único e sua
Propriedade (STIRNER, 1844). Ele sabia muito bem que estamos muito mais sozinhos do que
imaginamos.
Tal qual Stirner, tenho, como parte intrínseca do meu ser, a liberdade de pensamento;
até mesmo quando este traço, traz-me aborrecimentos, atuo como réu e juiz simultaneamente.
Posto o inverossímil em se resignar completamente à esta implacável realidade, cria-se, logicamente, devaneios cujos cenários dão falsa sensação de sentido à vida e redenção futura.
.... surpreendo a mim mesmo com a naturalidade com a qual narro minhas dores quando são os seus
atentos que captam meus fonemas e quando são os seus brilhantes olhos, que olham nos meus, com interesse e atenção.
Por isso mesmo, a meus amigos lhes digo: aqui estou, em liberdade novamente, lutando comigo mesmo para perpetuar meu pensamento libertário!!
E a vocês, meus inimigos, inúmeros parasitas dos quais tive o desprazer de conhecer, novamente faço a pergunta:
-Quem morrerá primeiro...????
Samuel Delmonte
02 de outubro de 2023
Há algo nos seus olhos que me intriga...
..., não sei ao certo o que é...
..., mas o que sim sei é que quando eles brilham, enfeitiçam-me.
Tenho vontade de lhe perguntar o que faz eles brilharem; contudo, falta-me, para tanto,
a audácia necessária.
Por outro lado, procuro detectar sutilmente os estímulos dos quais fazem eles (os seus olhos)
brilharem da mesma forma que as mais cintilantes estrelas de uma bela noite iluminada pela
luz que traz consigo o passado destes incríveis astros.
Assim como tais estrelas, parece-me que teus olhos refletem muito do seu passado, cujas dores fizeram com que seja mais madura que sua real idade.
Eles refletem também, doçura, sensibilidade e lealdade, sendo esta última qualidade preciosíssima e rara.
Certa vez Nietsche disse que se uma pessoa não possui alegria para transmitir ao próximo, tem em
contrapartida, algo mais valioso: a sua dor!
Sinto na minha quase extinta confiança nos seres humanos em geral, sobrevida quando compartilho a minha própria dor com ti...
.... surpreendo a mim mesmo com a naturalidade com a qual narro minhas dores quando são os seus
atentos que captam meus fonemas e quando são os seus brilhantes olhos, que olham nos meus, com interesse e atenção.
Einstein dizia que o tempo é uma ilusão; contudo, os lapsos temporais dos quais estou próximo a ti,
inundam-me de rara felicidade e satisfação.
Apesar disso, sei que sofrerei quando chegar a hora da despedida; lembrarei com carinho dos momentos em que tive sua companhia.
Muito provavelmente farei o mesmo que um personagem de Kafka, inúmeras vezes expressado por ele nos seus livros:
- Olharei pela janela, hora após hora, esperançoso que você, algum dia, passe por ela.
Lamento não haver conhecido alguém como você antes...
...e, se algum dia eu me deparar com o Anjo Caído, pedir-lhe-ei que reviva eternamente os dias dos quais passei junto a ti.
Despeço-me nesta singela carta citando Shakespeare:
“Cavalheiros...
Do seu eterno amigo e admirador,
Samuel Delmonte
04 de abril de 2023
Carta de Exibição apresentada `a comissão de seleção, como pré-requisito de ingresso ao curso de Mestrado
em Física-Matemática da USP.
25 de março de 2023
À comissão de seleção,
Chamo-me Samuel Capelozzi Delmonte Fernandes, 43, sou graduado em Análise e Desenvolvimento
de Sistemas pela Universidade Anhembi Morumbi, com especialização em Inteligência Artificial
pela Universidade Presbiteriana Mackenzie. Ambas as medias finais atingiram, reciprocamente,
as pontuações de 8,66 e 8,47; ademais, curso Bacharelado em Física na Unimes, situando-me no
quinto semestre. Em decorrência do desempenho proeminente, fui convidado para a monitoria das
graduações, tanto a concluída quanto a em vigor, as quais exerci. Eventualmente, ministro aulas
particulares de matemática e física para estudantes do ensino médio, para candidatos aos
vestibulares e concursos públicos, além de alunos da engenharia e química, que estejam cursando
do primeiro ao quarto semestre; fi-lo, ora através de instituições, ora autonomamente.
Das minhas maiores ambições acadêmicas, a Universidade de São Paulo sempre foi um requisito
fundamental para a concretização de tais avidezes; aliás, a USP esteve presente na minha
vida desde que nasci, literalmente, afinal, tenho no seio familiar, quatro membros graduados
por esta universidade. São eles, a minha mãe, Vera Luiza Capelozzi, professora associada
de patologia pulmonar, da faculdade de medicina, com mais de seiscentos trabalhos publicados,
ela está em atividade; além dela, seus irmãos mais novos, meus tios, Marco Antônio Capelozzi
e Marisa Capelozzi, são ambos doutores pela USP, ele no departamento de psiquiatria, ela no de
anestesia; e, finalmente, aquele que foi minha maior inspiração, meu querido pai, Carlos Alberto
Delmonte Fernandes, titulado, pela Universidade de São Paulo, como doutor em medicina legal;
infelizmente ele já não está, impossibilitando portanto, que desfrute deste momento comigo, o que certamente, o faria:
Oh, queridos pai e mãe... que fortuna a minha.
Interpreto o mundo de forma estoica, fato cuja implicação, grosso modo, fez com que eu precisasse sempre, desde a infância, de explicações realísticas aos eventos e fenômenos que, a mim, rodeavam. Desde cedo, dogmas preestabelecidos e dizeres pendurados em paredes, queriam, a mim, dizer nada. Não obstante, minha admiração e encanto pelas ciências físicas e matemáticas, crescia exponencialmente, tal qual o meu hábito de leitura. Na literatura, interesso-me, sobretudo, pelos autores do Romantismo Alemão, do século XIX, com ênfase em Arthur Schopenhauer, Soren Kierkegaard (dinamarquês), Friedrich Nietzsche, Max Stirner, além de Franz Kafka(checoslovaco) e Luiz Felipe Pondé (brasileiro). Tais filosofias, influenciaram a confecção do meu próprio livro, A Desordem – a arte de pensar com a própria cabeça, disponível nas melhores livrarias. Embora a obra seja constituída de ensaios filosóficos seu título principal, tem relação direta com a segunda lei da termodinâmica, afinal, parece-me verossímil supor, que os efeitos entrópicos atuam nas sociedades como um todo, fato que justificaria a não evolução comportamental dos seres humanos, além, é claro, de outros fatores. Das literaturas das ciências exatas, que felizmente conheci, destaco quatro autores, todos geniais, porquanto, dois deles puderam , ao meu ver, dissertar a respeito do embate entre relativismo determinista e probabilismo quântico da forma mais imparcial possível, fato raro; ambos ganharam o prêmio Nobel, sendo o primeiro Richard Feynman, com suas doze lições e o segundo é Murray Gell-Mann com o seu O quark e o jaguar; os dois cientistas influenciaram profundamente meu pensamento. Em seguida destaco um grande, talvez, o maior de todos, aquele que absorve toda minha admiração, o terceiro autor é nada mais do que Albert Einstein, cujas biografias e trabalhos, os li exaustivamente. Enfatizo a obra de Abraham Pais, sutil é o Senhor, rico no formalismo Geométrico Riemanniano, cujas proporções perpassam, até emergir a equação de campo relativista. O pensamento einsteiniano corrobora para traduzir a forma como vejo o mundo. Por fim, o quarto autor que saliento, apresentou-me a hipótese que justifica a .linha de pesquisa que pretendo optar, que diz respeito ao tempo e detalharei em dois breves parágrafos, ele
é o físico italiano Carlo Rovelli, cujas publicações, despertaram-me a coragem necessária para trilhar um árduo caminho do desconhecido, com a intuição de predizer como a natureza se manifesta, esperançoso em me deparar com aquilo que sabemos que não sabemos, ou quiçá, com maior fortuna,
deparar-me com aquilo que não sabemos que não sabemos.
Da minha formação, tornei-me, sobretudo, um programador; a graduação ressaltou minha identidade
profissional de Programador Front-End, com sólidos conhecimentos em linguagem de marcação HTML5,
linguagem de estilo CSS3 e linguagem de programação JAVASCRIPT, meus trabalhos, anexados aos documentos,
são feitos em código puro, um caractere de cada vez. Em todos eles há simuladores da Mecânica Clássica, programados com base no JASCRIPT e abundante utilização de sua biblioteca JQUERY; divirto-me, também, programando simuladores da função densidade de probabilidade normal, que a meu ver, é o rigor matemático escolhido pela Natureza, para assim, manifestar-se. Profissionalmente, programei, sob medida, a camada Front-End de lojas virtuais (E-Commerce); estive a cargo da gerência do departamento de sites da Editora Escala. Ademais, ministrei aulas particulares de matemática e física, como colaborador, citando a Educa Fácil SP como exemplo, exerci, obviamente, inumeráveis trabalhos na modalidade remota. Contudo, percebi que os recursos que dispunha, não eram os mais adequados para simular os fenômenos físicos, e posteriormente galgar uma posição acadêmica nas ciências mais puras, como a física e a matemática. A partir deste momento, decidi me aproximar do belíssimo contexto das equações, agregando ao meu perfil acadêmico e profissional, os dotes exigidos pelas ciências de dados, com atenção especial ao aprendizado de máquina; para tal proposito, dediquei-me ao aprendizado da linguagem de programação Python, poderosa o bastante para suprir minhas necessidades operacionais, já relatadas. Em vista disso, adquiri consistentes conhecimentos nas seguintes bibliotecas do universo Python: Numpy, Pandas, Matpolotlib, Scikit Learn, Sympy e Scipy. Na empreitada como cientista de dados, conclui uma Especialização em Inteligência Artificial, pela Universidade Presbiteriana Mackenzie; experiência que foi de grande valia na composição do meu conhecimento das máquinas que aprendem. Após essa jornada acadêmica, sinto-me apto para iniciar aquela trilha rumo ao desconhecido, e das palavras de Franz Kafka, quando afirmou que – deste ponto adiante, não há mais retorno – faço as minhas, ciente que há duas possibilidades de destino: rumo a lugar nenhum, ou rumo às profundezas da essência da Natureza, tal como ela é, implacavelmente indiferente para conosco.
Como síntese do que acima discursei, venho por meio desta, disponibilizar-me a ingressar no curso de Mestrado em Matemática Aplicada, alocado na área de pesquisa de Física-Matemática, especificamente na modalidade de Teoria Clássica e Quântica de Campos. Pretendo defender a tese de que a grandeza tempo não faz parte das fundamentais, mas sim de mensurações derivadas, ou talvez, descartável, do ponto de vista rigoroso da sintaxe matemática; parece-me que ele, o tempo, faz parte de um recurso cognitivo, possivelmente obrigatório, para que o córtex humano, codifique sucessões de eventos realísticos. Bem como Hernri Poincaré, celebre matemático e entusiasta do rebaixamento do status temporal, costumava dizer que o tempo não poderia ser fundamental, do ponto de vista físico, pois não é mensurável por meio da consciência unicamente, diferentemente das outras, basta tentar contabilizar com a mente algumas horas e, certamente haverá erro grosseiro de precisão, ou tentar interpretar o resultado fenológico duma variação do que chamamos tempo, de milhões ou bilhões. A ausência do tempo, poderia desmoronar diversos problemas entre o relativo e o quântico, desprezaria conceitos, as vezes prolixos em demasia, tal como a ideia de início, e, quem sabe, nos conduziria à concretização do sonho dos antigos, que desde os seus ombros, encontraríamos uma harmônica relação simétrica das Teorias da Relatividade e Quântica, quando se refere ao emaranhamento quântico e seu resultante colapso. Os testes da hipótese serão feitos através de uma rede neural, construída com Python, e calibrada para predizer e sugerir formalismos (equações) com baixo de teor de complexidade com respeito às Teorias da Relatividade e Quântica de campos. O meu Trabalho de Conclusão de Curso é um embrião desta empreitada.
Sem mais o que dizer, oferto desde meus esforços, conduzir o Mestrado com base no método cientifico ortodoxo, herdado da redução analítica de René Descartes e do método indutivo de Roger Bacon, oferto, também a capacidade, que possuo, de rápido aprendizado, além de profunda devoção às equações, afinal somente elas atingem a eternidade.
Não basta apreciar a beleza de um jardim, sem ter que imaginar que há fadas nele? (Douglas Adams)
Samuel Delmonte
01 de março de 2023
“Guardemos no mais profundo de nós mesmos uma certeza superior a todas as outras:
a vida não tem sentido, não pode tê-lo. Emil Cioran” – (Emil Cioran)
O meu caminho, esse sim, será rumo a lugar nenhum...
...durante a jornada, cumprida com passos desconexos, ...
...dissipa-se, com o dilatar do tempo, as memorias de um passado, já inacessível, ...
...rumo a um invariável futuro frio e vaporoso...
Com esta regência, se manifesta a Natureza, austera e elegante, propulsora duma realidade aleatória...
...cuja contingência esclarece a atroz indiferença dela (da Natureza) com entidades, vivas ou não.
Conjuntura estoica, cuja severidade, seleciona poucos capazes de reconhecer o caráter factual do Universo...
...e, resignar-se `a uma breve existência, desprovida de sentido pré-estabelecido e fim irrevogável e equipolente a todos.
Definitivamente não haverá salvação, pois o ultimo derradeiro, de qualquer um, será um fracasso final, antecessor da inexistência.
Samuel Delmonte
23 de janeiro de 2023
“O futebol é a coisa mais importante, das coisas menos importantes.” – (Milton Neves)
Após a morte de Pelé, o maior de todos, restaram cinco jogadores vivos, dos 21 integrantes
do elenco da seleção brasileira, campeã da Copa do Mundo, de 1958, realizada na Suécia.
O atleta do século, que recém repousa, esvaiu-se aos 82 anos, embora fora o mais jovem componente do escrete canarinho, afinal de contas, completava 17 anos, oito meses e 6 dias, durante a final daquela copa, realizada em Solna, em 29 de junho de 1958.
É, portanto, óbvio concluir, que os tais cinco jogadores, ainda vivos após, quase 65 anos, possuem, obrigatoriamente, mais de 82 anos, além de, apenas haver sido titular de fato, um deles.
Porquanto, estão ainda vivos:
1-Dino Sani , 90 anos, volante
2-Mazzola, 84 anos, atacante, 2 gols - 1° partida
3- Moacir,86 anos, meia
4 - Pepe , 87 anos, ponta-esquerda
5 - Zagallo , 91 anos, ponta-esquerda, titular , 1 gol - 6° partida
Já morreram:
Samuel Delmonte
Parte 02 - Deslocamento temporal da função de onda¶
a equação da função de onda completa:¶
O opH é um operador de evolução temporal. Pode,ele, também assumir, a seguinte identidade matemática:¶
$$\text{op }U(\Delta t)=e^{\frac{-i\text{ op }H}{\hbar}}$$
Resultando, portanto, na solução, descrita abaixo:¶
Podendo tratar o expoente de um operador, por meio de uma série infinita, tem-se:¶
$$e^{\frac{-i\text{ op }H\Delta t}{\hbar}}=\sum_{n}\frac{\Big(\frac{-i\text{ op }H\Delta t}{\hbar}\Big)^{n}}{n!}$$
#Bibliotecas
import matplotlib.animation as animation
from IPython.display import HTML
import matplotlib.pyplot as plt
import scipy.fftpack as fft
import scipy.linalg as scl
import numpy as np
import math
%matplotlib widget
%matplotlib inline
O Halmitoniano no espaço:¶
Os valores de entrada:¶
hbar = 1
m = 1
N = 2**11
L = 200.0
step_low = 0.
step_high= 1.
V0 = 10.
Definição do espaço:¶
n = np.arange(N)
x0 = -L/2.
xN = L/2.
Delta_x = (xN - x0)/N
print("Delta_x = ",Delta_x)
x = x0 + n*Delta_x
Delta_x = 0.09765625
Definição do potencial:¶
V = np.zeros(N)
for i in range(N):
if x[i]>= step_low and x[i]<= step_high:
V[i]= V0
Configuração do Hamiltoniano para a função
V, multiplicação com a matriz inversa:¶Mdd = 1./(Delta_x**2)*(np.diag(np.ones(N-1),-1)
- 2* np.diag(np.ones(N),0)
+ np.diag(np.ones(N-1),1))
H = -(hbar*hbar)/(2.0*m)*Mdd + np.diag(V)
En,psiT = np.linalg.eigh(H) # autovalores e os autovetores.
psi = np.transpose(psiT) # Tomamos a transposta de psiT para os vetores de função de onda
# que podem ser acessados como psi[n]
Intervalo temporal¶
dt_max = 2/np.max(En) # Critério de estabilidade.
dt = 0.001
if dt > dt_max:
print("ATENÇÃO: dt está na região instável!")
Função de onda inicial¶
g_x0=-10.
g_k0=6.
g_sig=2.
Definição de um Gaussiano no espaço K, com $p=\hbar k$, um momento $k_{0} $, e o espaço x, $\psi(x,0)=\big(\frac{2L}{\pi}\big)^{1/4}\cdot e^{-Lx^{2}}$:¶
def psi0(x,g_x0,g_k0,g_sig):
_Norm_x=np.sqrt(Delta_x/g_sig)/(np.pi**0.25)
return(_Norm_x*np.exp(-(x-g_x0)**2/(2.*g_sig*g_sig)+1j*g_k0*x))
psi_t0 = psi0(x,g_x0,g_k0,g_sig)
# H é Hermitiano?
print("Verifique se H é realmente Hermitiano : ",np.array_equal(H.conj().T,H))
Verifique se H é realmente Hermitiano : True
Ut_mat = np.diag(np.ones(N,dtype="complex128"),0)
print("Criação de uma matriz U(dt = {})".format(dt))
for n in range(1,3):
# Realiza a soma. Como se trata de matrizes, o processo irá demorar se N for grande.
Ut_mat += np.linalg.matrix_power((-1j*dt*H/hbar),n)/math.factorial(n)
Criação de uma matriz U(dt = 0.001)
p = Ut_mat.dot(psi_t0)
print("O quanto a normalização muda por etapa? Desde {} até {}".format(np.linalg.norm(psi_t0),np.linalg.norm(p)))
print("Nº de etapas em que a norma está errada por um fator 2 : ",1/(np.linalg.norm(p)-1))
O quanto a normalização muda por etapa? Desde 1.0 até 1.0000000127814086
Nº de etapas em que a norma está errada por um fator 2 : 78238637.96537858
teste do movimento gaussiano:¶
psi_t0 = psi0(x,g_x0,g_k0,g_sig)
psi_t1 = psi_t0
psi_tu = []
for t in range(3500):
psi_t1 = Ut_mat.dot(psi_t1)
if t>0 and t%500==0:
psi_tu.append( (t,psi_t1))
psi_tu.append( (t,psi_t1))
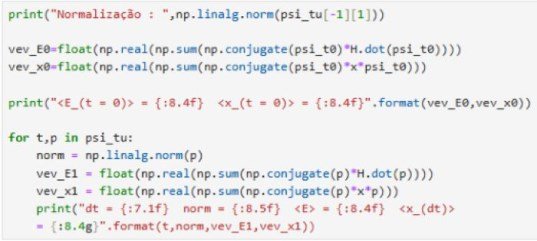
print("Normalização : ",np.linalg.norm(psi_tu[-1][1]))
vev_E0=float(np.real(np.sum(np.conjugate(psi_t0)*H.dot(psi_t0))))
vev_x0=float(np.real(np.sum(np.conjugate(psi_t0)*x*psi_t0)))
print("<E_(t = 0)> = {:8.4f} <x_(t = 0)> = {:8.4f}".format(vev_E0,vev_x0))
for t,p in psi_tu:
norm = np.linalg.norm(p)
vev_E1 = float(np.real(np.sum(np.conjugate(p)*H.dot(p))))
vev_x1 = float(np.real(np.sum(np.conjugate(p)*x*p)))
print("dt = {:7.1f} norm = {:8.5f} <E> = {:8.4f} <x_(dt)> = {:8.4g}".format(t,norm,vev_E1,vev_x1))
Normalização : 1.000044736361259
<E_(t = 0)> = 17.5429 <x_(t = 0)> = -10.0000
dt = 500.0 norm = 1.00001 <E> = 17.5432 <x_(dt)> = -7.164
dt = 1000.0 norm = 1.00001 <E> = 17.5434 <x_(dt)> = -4.335
dt = 1500.0 norm = 1.00002 <E> = 17.5436 <x_(dt)> = -1.55
dt = 2000.0 norm = 1.00003 <E> = 17.5439 <x_(dt)> = 0.8044
dt = 2500.0 norm = 1.00003 <E> = 17.5441 <x_(dt)> = 2.91
dt = 3000.0 norm = 1.00004 <E> = 17.5443 <x_(dt)> = 5.103
dt = 3499.0 norm = 1.00004 <E> = 17.5446 <x_(dt)> = 7.305
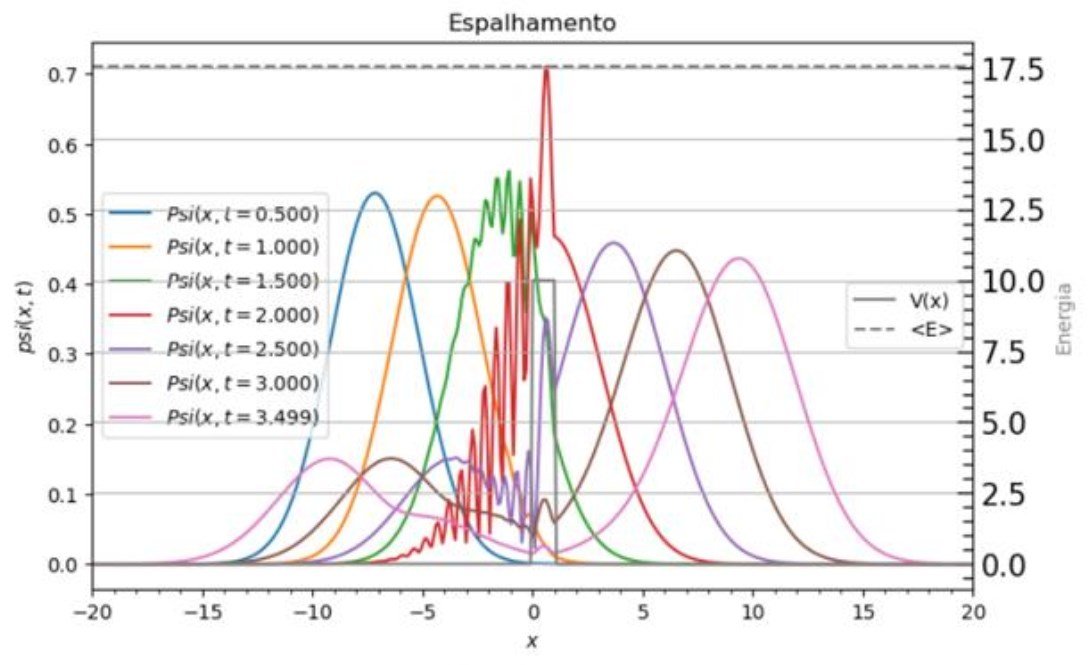
Dos dados obtidos, resulta:¶
def opt_plot():
plt.minorticks_on()
plt.tick_params(axis='both',which='minor', direction = "in",
top = True,right = True, length=5,width=1,
labelsize=15)
plt.tick_params(axis='both',which='major', direction = "in",
top = True,right = True, length=8,width=1,
labelsize=15)
plt.figure(figsize=(8,5))
if vev_E0>max(V):
plt.title('Espalhamento')
else:
plt.title('Tunelamento')
plt.ylabel('$psi(x,t)$')
plt.xlabel('$x$')
# plt.plot(x,np.abs(psi_t0)/np.sqrt(Delta_x),label="$\Psi(x,t=0)$")
for t,p in psi_tu:
plt.plot(x,np.abs(p)/np.sqrt(Delta_x),label="$Psi(x,t={:6.3f})$".format(t*dt))
plt.legend(loc = 'center left')
ax1 = plt.twinx()
plt.plot(x,V,color="grey",label="V(x)")
plt.plot([x[0],x[N-1]],[vev_E0,vev_E0],color="grey",linestyle="--",label="<E>")
plt.ylabel("Energia",color="grey")
plt.xlim(g_x0-5*g_sig,-g_x0+5*g_sig)
plt.legend(loc='best')
plt.grid()
opt_plot()
plt.savefig('Estado deslocado.png')
%time Ut_05s = np.linalg.matrix_power(Ut_mat,int(0.5/dt) )
CPU times: total: 7min 6s
Wall time: 2min
Repetição de tarefa¶
psi_t0 = psi0(x,g_x0,g_k0,g_sig)
psi_t1 = psi_t0
psi_tu05 = []
for t in range(7):
psi_t1 = Ut_05s.dot(psi_t1)
psi_tu05.append( (t,psi_t1))
# psi_tu.append( (t,psi_t1))
print("Start")
v1=[]
v2=[]
tm=[]
count=0
for t,p in psi_tu05:
norm = np.linalg.norm(p)
vev_E1 = float(np.real(np.sum(np.conjugate(p)*H.dot(p))))
vev_x1 = float(np.real(np.sum(np.conjugate(p)*x*p)))
v1.append(vev_E1)
v2.append(vev_x1)
tm.append(count)
count=count+1
print("dt = {:7.1f} norm = {:8.5f} <E> = {:8.4f} <x_(dt)> = {:8.4g}".format(t,norm,vev_E1,vev_x1))
Start
dt = 0.0 norm = 1.00001 <E> = 17.5432 <x_(dt)> = -7.17
dt = 1.0 norm = 1.00001 <E> = 17.5434 <x_(dt)> = -4.34
dt = 2.0 norm = 1.00002 <E> = 17.5436 <x_(dt)> = -1.555
dt = 3.0 norm = 1.00003 <E> = 17.5439 <x_(dt)> = 0.8002
dt = 4.0 norm = 1.00003 <E> = 17.5441 <x_(dt)> = 2.905
dt = 5.0 norm = 1.00004 <E> = 17.5443 <x_(dt)> = 5.099
dt = 6.0 norm = 1.00004 <E> = 17.5446 <x_(dt)> = 7.305
plt.figure(figsize=(8,5))
if vev_E0>max(V):
plt.title('Espalhamento')
else:
plt.title('Tunelamento')
plt.ylabel('$psi(x,t)$')
plt.xlabel('$x$')
line, = plt.plot(x,np.abs(psi_t0)/np.sqrt(Delta_x),label="$Psi(x,t=0)$")
for t,p in psi_tu05:
plt.plot(x,np.abs(p)/np.sqrt(Delta_x),label="$Psi(x,t={:6.3f})$".format(t*dt))
plt.legend(loc='center left')
ax1 = plt.twinx()
plt.plot(x,V,color="grey",label="V(x)")
plt.plot([x[0],x[6]],[vev_E0,vev_E0],color="grey",linestyle="--",label="<E>")
plt.ylabel("Energia",color="grey")
plt.xlim(g_x0-5*g_sig,-g_x0+5*g_sig)
plt.legend(loc='best')
plt.grid()
opt_plot()
plt.savefig('Estado deslocado - Pré-computados.png')
Parte 3 - A Regressão Simbólica¶
from sklearn.utils import check_random_state, shuffle
from gplearn.genetic import SymbolicRegressor
from sklearn.ensemble import RandomForestRegressor
from sklearn.tree import DecisionTreeRegressor
from sklearn.utils.random import check_random_state
from mpl_toolkits.mplot3d import Axes3D
from IPython.display import Image
import pydot
import graphviz
from sympy import *
import pandas as pd
Definição dos Operadores¶
converter = {
'sub': lambda x, y : x - y,
'div': lambda x, y : x/y,
'mul': lambda x, y : x*y,
'add': lambda x, y : x + y,
'neg': lambda x : -x,
'pow': lambda x, y : x**y,
'sin': lambda x : sin(x),
'cos': lambda x : cos(x),
'inv': lambda x: 1/x,
'sqrt': lambda x: x**0.5,
'pow3': lambda x: x**3
}
Interpretação Probabilística Gaussiana da Distribuição Normal¶
$$N(\mu,\sigma^{2})=\frac{1}{\sqrt{2\pi\sigma^{2}}}\cdot e^{-\frac{1}{2}\frac{(x-\mu)}{\sigma}^{2}}$$m1=[]
md=[]
count=0
tem=0
df=pd.DataFrame()
df2=pd.DataFrame()
xix=[]
df['v1']=v1
df2['v2']=v2
for i in v2:
m1.append(i)
tem=i-vev_x0
md.append(tem**2)
df['m1']=md
df2['t']=tm
dp=2.83/3
A = [float(i) for i in m1]
for i in A:
xix=np.linspace(-(3.*dp),(3.*dp),40)
y=0.39*(2.76**(-0.5*(xix**2)))
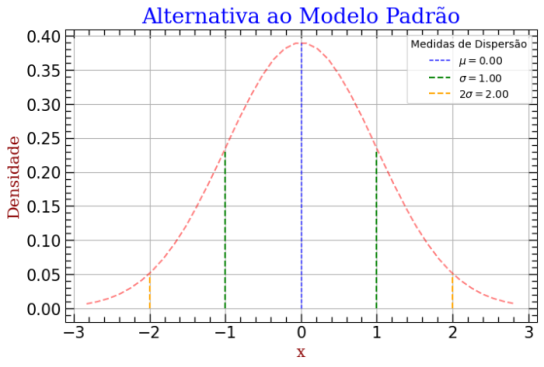
A amostra acima, resulta:¶
def opt_plot():
plt.minorticks_on()
plt.tick_params(axis='both',which='minor', direction = "in",
top = True,right = True, length=5,width=1,
labelsize=15)
plt.tick_params(axis='both',which='major', direction = "in",
top = True,right = True, length=8,width=1,
labelsize=15)
plt.figure(figsize=(8,5))
textstr = '\n'.join((
r'$\mu=%.2f$' % (0, ),
))
textstr02 = '\n'.join((
r'$\sigma=%.2f$' % (1, ),
))
textstr03 = '\n'.join((
r'$\sigma=%.2f$' % (2, ),
))
textstr04 = '\n'.join((
r'$\sigma=%.2f$' % (1, ),
r'$\mu=%.2f$' % (0, ),
))
plt.vlines(0, 0, 0.39, linestyle='dashed', color='b', linewidth=1, label=str(textstr)) # vlines(posição, início, fim)
plt.vlines(1, 0, 0.23, linestyle='dashed', color='green', linewidth=1.5, label= str(textstr02)) # vlines(posição, início, fim)
plt.vlines(-1, 0, 0.23, linestyle='dashed', color='green', linewidth=1.5) # vlines(posição, início, fim)
plt.vlines(2, 0, 0.05, linestyle='dashed', color='orange', linewidth=1.5, label= '2'+str(textstr03)) # vlines(posição, início, fim)
plt.vlines(-2, 0, 0.05, linestyle='dashed', color='orange', linewidth=1.5) # vlines(posição, início, fim)
font1 = {'family':'serif','color':'blue','size':20}
font2 = {'family':'serif','color':'darkred','size':15}
plt.title("Alternativa ao Modelo Padrão", fontdict = font1)
plt.xlabel("x", fontdict = font2)
plt.ylabel("Densidade", fontdict = font2)
plt.legend(title='Medidas de Dispersão')
plt.grid()
opt_plot()
plt.plot(xix,y ,'r--', alpha=0.5, label= textstr04)
[<matplotlib.lines.Line2D at 0x11c3e679d60>]
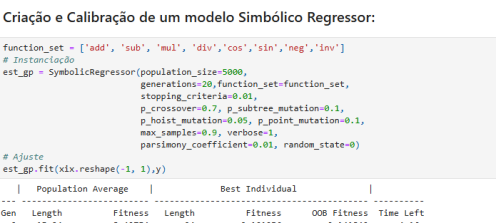
Criação e Calibração de um modelo Simbólico Regressor:¶
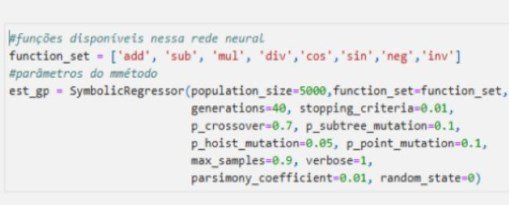
function_set = ['add', 'sub', 'mul', 'div','cos','sin','neg','inv']
# Instanciação
est_gp = SymbolicRegressor(population_size=5000,
generations=20,function_set=function_set,
stopping_criteria=0.01,
p_crossover=0.7, p_subtree_mutation=0.1,
p_hoist_mutation=0.05, p_point_mutation=0.1,
max_samples=0.9, verbose=1,
parsimony_coefficient=0.01, random_state=0)
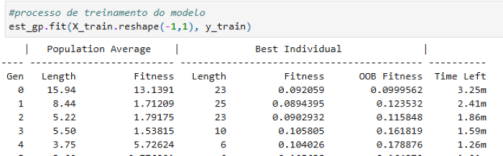
# Ajuste
est_gp.fit(xix.reshape(-1, 1),y)
| Population Average | Best Individual |
---- ------------------------- ------------------------------------------ ----------
Gen Length Fitness Length Fitness OOB Fitness Time Left
0 15.94 8.42754 24 0.101256 0.141842 3.93m
1 8.38 1.41838 10 0.0282817 0.0287366 4.66m
2 4.25 0.913171 10 0.0275074 0.0357058 2.07m
3 2.38 0.458598 10 0.0262319 0.0471853 1.69m
4 2.34 69.5123 10 0.0262295 0.0472067 1.69m
5 4.42 1.11605 11 0.0181481 0.0271488 2.21m
6 6.21 1.40624 11 0.0183373 0.0356987 2.37m
7 6.89 1.00531 11 0.0196629 0.0237683 1.42m
8 7.20 0.86294 11 0.0185499 0.0337846 1.46m
9 7.36 0.927227 12 0.0193277 0.0303689 1.27m
10 7.54 1.14538 12 0.0202671 0.0219142 1.03m
11 7.90 1.22699 8 0.0258667 0.038024 1.21m
12 8.04 1.22625 8 0.0252462 0.0436084 57.18s
13 7.96 1.29076 8 0.0249788 0.0460152 1.27m
14 7.86 1.30819 8 0.0245602 0.04586 1.12m
15 8.06 1.22489 8 0.0247419 0.0481478 46.88s
16 7.99 1.55607 8 0.0246505 0.04897 36.24s
17 7.92 1.26517 11 0.0241093 0.0259531 23.80s
18 7.97 1.25025 8 0.0246505 0.04897 7.76s
19 8.00 1.2177 10 0.023813 0.0384339 0.00s
div(0.333, sub(0.812, neg(mul(mul(0.696, X0), X0))))
In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.div(0.333, sub(0.812, neg(mul(mul(0.696, X0), X0))))
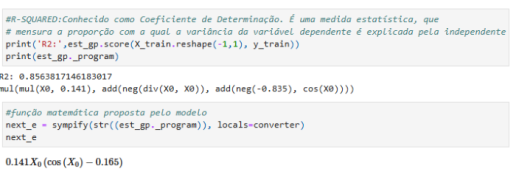
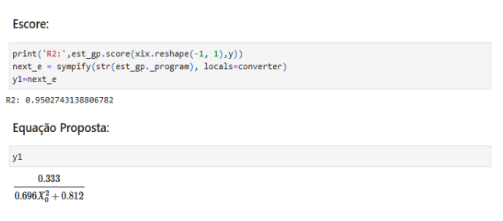
Escore:¶
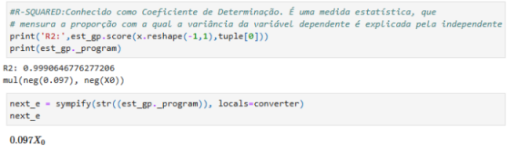
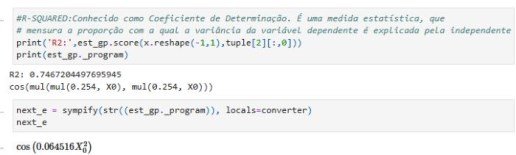
print('R2:',est_gp.score(xix.reshape(-1, 1),y))
next_e = sympify(str(est_gp._program), locals=converter)
y1=next_e
R2: 0.9502743138806782
Equação Proposta:¶
y1
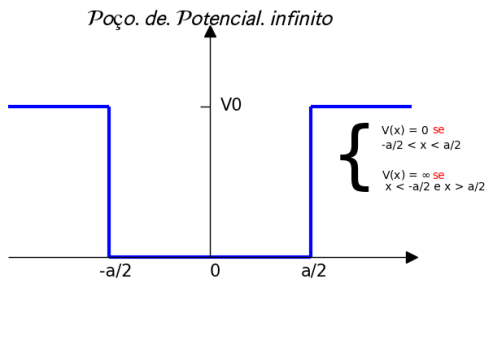
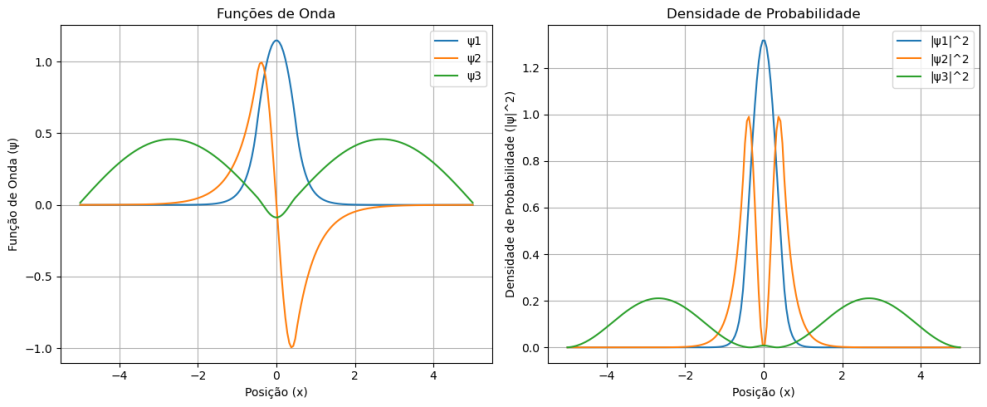
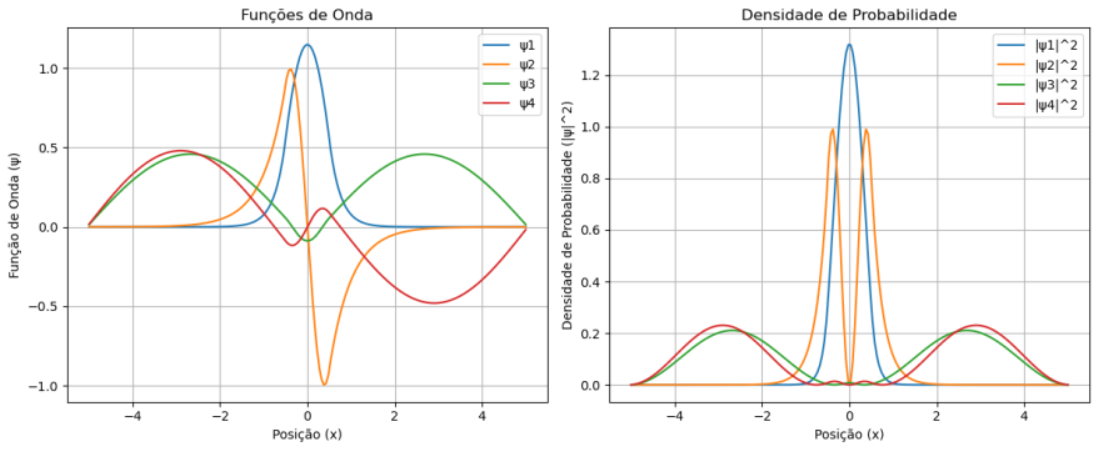
Soluções para o Poço de Potencial Infinito¶
Solução da função de onda da posição¶
$$ \psi_n(x) = \sqrt{\frac{2}{L}} \sin\left(\frac{n\pi x}{L}\right)$$
import matplotlib.pyplot as plt
import numpy as np
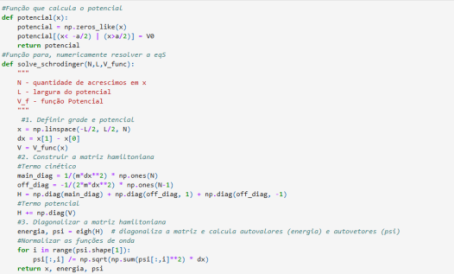
def opt_plot():
plt.minorticks_on()
plt.tick_params(axis='both',which='minor', direction = "in",
top = True,right = True, length=5,width=1,
labelsize=15)
plt.tick_params(axis='both',which='major', direction = "in",
top = True,right = True, length=8,width=1,
labelsize=15)
a=20
A=np.sqrt(2/a)
# Data for plotting
for i in range(5):
t = np.arange(0.0, 2.0, 0.01)
s = A*np.sin(0 * np.pi * t)
s1 = A*+np.sin(0.5 * np.pi * t)
s2 = A*np.sin(1.0 * np.pi * t)
s3 = A*np.sin(1.5 * np.pi * t )
s4 = A*np.sin(2.0 * np.pi * t)
fig, ax = plt.subplots(figsize=(10,6))
ax.plot(t, s)
ax.plot(t, s1,label='n=0')
ax.plot(t, s2,label='n=1')
ax.plot(t, s3,label='n=2')
ax.plot(t, s4,label='n=3')
ax.set(xlabel='time (s)', ylabel='$w(x,t)$',
title="Soluções para o Poço de Potencial Infinito")
ax.grid()
opt_plot()
plt.legend()
fig.savefig("test.png")
plt.show()
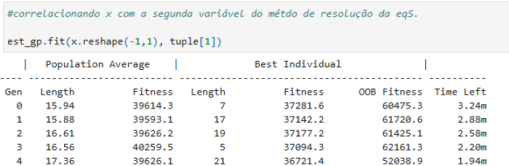
Gera-se e ajusta-se,um modelo Simbólico Regressor para a solução da função de onda da Posição:¶
est_gp.fit(t.reshape(-1, 1),s1)
| Population Average | Best Individual |
---- ------------------------- ------------------------------------------ ----------
Gen Length Fitness Length Fitness OOB Fitness Time Left
0 15.94 10.9162 6 0.0305686 0.0286007 4.07m
1 8.25 1.36407 9 0.0238001 0.0246281 2.44m
2 5.03 0.916274 9 0.0248264 0.0153917 3.08m
3 2.76 0.458664 7 0.0265144 0.031241 1.97m
4 2.38 16.2677 7 0.026512 0.0312625 2.16m
5 5.04 0.628504 6 0.0142702 0.0251 1.99m
6 6.00 1.07399 6 0.0145615 0.0224778 1.42m
7 6.08 0.645816 6 0.0137287 0.0299735 2.52m
8 6.07 0.686379 6 0.013608 0.0310599 2.07m
9 6.19 0.767054 6 0.0124938 0.0410876 2.18m
10 6.10 0.799589 6 0.0129802 0.0367098 1.99m
11 6.08 0.641764 6 0.013121 0.0354423 1.06m
12 6.19 0.677095 6 0.0122761 0.0430471 2.23m
13 6.17 0.895997 6 0.012991 0.0366123 1.28m
14 6.06 0.736398 6 0.0132391 0.03438 41.61s
15 6.18 0.696137 6 0.0133269 0.0335893 35.80s
16 6.17 0.844118 6 0.0132413 0.0343599 24.23s
17 6.09 0.700994 6 0.0128263 0.0380947 12.49s
18 6.16 0.612862 6 0.0130871 0.0357479 8.11s
19 6.17 0.633526 6 0.0125276 0.0407834 0.00s
add(mul(-0.517, X0), sin(X0))
In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.add(mul(-0.517, X0), sin(X0))
Escore¶
print('R2:',est_gp.score(t.reshape(-1, 1),s1))
next_e = sympify(str(est_gp._program), locals=converter)
y2=next_e
R2: 0.9048979343134357
Equação Proposta¶
y2
import numpy as np
a=1
h=1
m=1
En=0
Enn=[]
for i in range(7):
En=((i**2)*(h**2)*(np.pi**2))/(2*m*a*a)
Enn.append(En)
for i in range(7):
n = i+1
print("E[{}] = {:9.4f}".format(n,Enn[i],n, n*n*np.pi**2*h*h/(2*m*a*a)))
E[1] = 0.0000
E[2] = 4.9348
E[3] = 19.7392
E[4] = 44.4132
E[5] = 78.9568
E[6] = 123.3701
E[7] = 177.6529
Gráfico da Energia Quantizada:¶
def opt_plot():
plt.minorticks_on()
plt.tick_params(axis='both',which='minor', direction = "in",
top = True,right = True, length=5,width=1,
labelsize=15)
plt.tick_params(axis='both',which='major', direction = "in",
top = True,right = True, length=8,width=1,
labelsize=15)
plt.figure(figsize=(10, 6))
plt.plot(Enn)
plt.text(x=0.0, y=10, s="Eo", weight="bold")
plt.text(x=1.0, y=15, s="E1", weight="bold")
plt.text(x=2.0, y=30, s="E2", weight="bold")
plt.text(x=3.0, y=55, s="E3", weight="bold")
plt.text(x=4.0, y=90, s="E4", weight="bold")
plt.text(x=5.0, y=135, s="E5", weight="bold")
plt.text(x=6.0, y=170, s="E6", weight="bold")
for i in range(7):
En=((i**2)*(h**2)*(np.pi**2))/(2*m*a*a)
plt.scatter(i,En, marker='o',label="E["+str(i)+"] = "+str(round(Enn[i],2)))
font1 = {'family':'serif','color':'blue','size':20}
font2 = {'family':'serif','color':'darkred','size':15}
plt.title("Níveis Energéticos", fontdict = font1)
plt.xlabel("n", fontdict = font2)
plt.ylabel("Energia", fontdict = font2)
plt.text(x=2.0, y=130, s=r'$f(x) = 4.93.{x^2}$',fontdict = font2)
plt.legend(title='Níveis de Energia')
opt_plot()
plt.grid()
Para:¶
l_count=np.linspace(0,6,7)
E_df=np.array([l_count,Enn])
E_df02=E_df.T
E_df02
y_E=4.93*E_df[:,0]**2
Obtem-se o seguinte modelo:¶
function_set = ['add', 'sub', 'mul', 'div','cos','sin','neg','inv']
# Instanciação
est_gp = SymbolicRegressor(population_size=5000,
generations=20,function_set=function_set,
stopping_criteria=0.01,
p_crossover=0.7, p_subtree_mutation=0.1,
p_hoist_mutation=0.05, p_point_mutation=0.1,
max_samples=0.9, verbose=1,
parsimony_coefficient=0.01, random_state=0)
# Ajuste
est_gp.fit(E_df,y_E)
| Population Average | Best Individual |
---- ------------------------- ------------------------------------------ ----------
Gen Length Fitness Length Fitness OOB Fitness Time Left
0 10.86 1.23511e+07 14 0 0 2.13m
neg(neg(div(mul(inv(X0), mul(X1, -0.362)), sub(cos(X2), sin(0.200)))))
In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.neg(neg(div(mul(inv(X0), mul(X1, -0.362)), sub(cos(X2), sin(0.200)))))
Cujo Escore é:¶
next_e = sympify(str(est_gp._program), locals=converter)
y3=next_e
com a proposta de equação:¶
y3
Densidade de Probabilidade da posição¶
$$|\psi_n(x)|^{2} = {\frac{2}{a}} \sin^{2}(n\pi x)$$
import matplotlib.pyplot as plt
import numpy as np
def opt_plot():
plt.minorticks_on()
plt.tick_params(axis='both',which='minor', direction = "in",
top = True,right = True, length=5,width=1,
labelsize=15)
plt.tick_params(axis='both',which='major', direction = "in",
top = True,right = True, length=8,width=1,
labelsize=15)
val_esp=[-7.17,-4.344,-1.555,0.8002,2.905,5.095 ,7.305]
a=20
A=(2/a)
# Data for plotting
t = np.arange(0.0, 2.0, 0.01)
x=np.arange(0.0,2.0,0.01)
s = A*(np.sin((0 * np.pi * x)))**2
s1 = A*(np.sin((0.5 * np.pi * abs(x))))**2
s2 = A*(np.sin((1.0 * np.pi * x)))**2
s3 = A*(np.sin((1.5 * np.pi * x)))**2
s4 = A*(np.sin((2.0 * np.pi * x)))**2
fig, ax = plt.subplots(figsize=(10,6))
ax.plot(x, s)
ax.plot(x, s1)
ax.fill(x,s1,color='grey', alpha=0.5, label='n1')
ax.plot(x, s2)
ax.fill(x,s2,color='blue', alpha=0.5, label='n2')
ax.plot(x, s3)
ax.fill(x,s3,color='green', alpha=0.5, label='n3')
ax.plot(x, s4)
ax.fill(x,s4,color='yellow', alpha=0.3, label='n4')
ax.set(xlabel='time (s)', ylabel='$w(x,t)$',
title="Densidade de Probabilidade da Posição")
ax.grid()
ax.legend()
opt_plot()
fig.savefig("test.png")
plt.show()
Relaciona-se os valores médios esperados, da funçao de onda, com a função normal gaussiana:¶
val_esp=np.array([-7.17,-4.344,-1.555,0.8002,2.905,5.095 ,7.305])
niveis=[0,1,2,3,4,5,6]
arr_value=np.array([[niveis],[val_esp]])
x_arr = val_esp
print(x_arr)
y_arr=0.399*(2.76**(-0.5*x_arr[:]**2))
[-7.17 -4.344 -1.555 0.8002 2.905 5.095 7.305 ]
para então, modular:¶
function_set = ['add', 'sub', 'mul', 'div','cos','sin','neg','inv']
# Instanciação
est_gp = SymbolicRegressor(population_size=5000,
generations=20,function_set=function_set,
stopping_criteria=0.01,
p_crossover=0.7, p_subtree_mutation=0.1,
p_hoist_mutation=0.05, p_point_mutation=0.1,
max_samples=0.9, verbose=1,
parsimony_coefficient=0.01, random_state=0)
# Ajuste
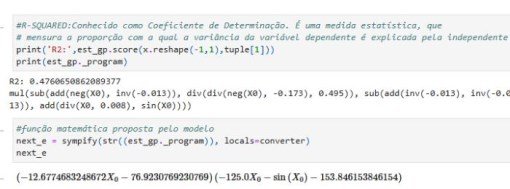
est_gp.fit(x_arr.reshape(-1,1),y_arr)
| Population Average | Best Individual |
---- ------------------------- ------------------------------------------ ----------
Gen Length Fitness Length Fitness OOB Fitness Time Left
0 15.94 24.2581 9 0.0150923 0.125521 2.42m
1 9.25 3.10342 29 0.001741 0.390678 2.71m
sin(mul(cos(sub(sin(add(0.782, 0.138)), sin(sub(0.773, X0)))), div(cos(inv(cos(X0))), sub(sin(add(-0.483, 0.614)), mul(mul(X0, X0), add(X0, X0))))))
In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.sin(mul(cos(sub(sin(add(0.782, 0.138)), sin(sub(0.773, X0)))), div(cos(inv(cos(X0))), sub(sin(add(-0.483, 0.614)), mul(mul(X0, X0), add(X0, X0))))))
Escore:¶
print('R2:',est_gp.score(x_arr.reshape(-1,1),y_arr))
next_e = sympify(str(est_gp._program), locals=converter)
y2_arr=next_e
R2: -1.099778938698206
Equaçao:¶
y2_arr
O desvio padrão da posição:¶
$$\Delta xn ={\sqrt{ <x^{2}n> - <xn>^{2}}} = a{\sqrt{{\frac{1}{12}}- {\frac{1}{2\pi^{2}n^{2}}}}} $$
import pandas as pd
xx0=-10
val_esp=[-7.17,-4.344,-1.555,0.8002,2.905,5.095 ,7.305]
a=val_esp[6]-val_esp[0]
x_quadrado=0
dp=[]
n=1
desp=0
j=-10
c=0
dsp=[]
for i in val_esp:
if (j<0 and i>0):
c=np.abs(j)+i
else:
c=np.abs(j)-np.abs(i)
c=np.abs(c)
dsp.append(c)
j=i
dsp
er_count=0
err=[]
med_ex=2.86
for i in dsp:
er_count=med_ex-i
err.append(er_count)
err
dpp=pd.DataFrame()
dpp['DesvioP']=dsp
dpp['ErrDesvioP']=err
dpp
DesvioP
ErrDesvioP
0
2.8300
0.0300
1
2.8260
0.0340
2
2.7890
0.0710
3
2.3552
0.5048
4
2.1048
0.7552
5
2.1900
0.6700
6
2.2100
0.6500
Podemos encontrar, também, o desvio padrão do momento¶
$$e^{\frac{-i\text{ op }H\Delta t}{\hbar}}=\sum_{n}\frac{\Big(\frac{-i\text{ op }H\Delta t}{\hbar}\Big)^{n}}{n!}$$$$\Delta Kn = <K^{2}n> - <Kn>^{2} = {\frac{n\hbar}{a}} $$
import numpy as np
a=20
h=1
dpm=0
dmp=[]
for i in range(7):
a=np.abs(a)
dpm=(i*np.pi)/a
dmp.append(dpm)
O Princípio da Incerteza¶
$$\Delta x.\Delta p >\frac{\hbar}{2}$$
desvf=pd.DataFrame()
desvf["dp"]=dpp.DesvioP
desvf["dmp"]=dmp
j=0
incerteza=[]
form=[]
f=r'$\Delta x.\Delta p $'
g=r'$\Delta x $'
h=r'$\Delta p $'
c=0
gord=dpp.DesvioP
hord=dmp
for i in dpp.DesvioP:
j=dmp[c]*i
incerteza.append(j)
form.append(f)
c=c+1
desvf02=pd.DataFrame()
desvf02[g]=gord
desvf02[h]=hord
desvf02["lesquerdo"]=form
desvf02["incerteza"]=incerteza
desvf02
$\Delta x $
$\Delta p $
lesquerdo
incerteza
0
2.8300
0.000000
$\Delta x.\Delta p $
0.000000
1
2.8260
0.157080
$\Delta x.\Delta p $
0.443907
2
2.7890
0.314159
$\Delta x.\Delta p $
0.876190
3
2.3552
0.471239
$\Delta x.\Delta p $
1.109862
4
2.1048
0.628319
$\Delta x.\Delta p $
1.322485
5
2.1900
0.785398
$\Delta x.\Delta p $
1.720022
6
2.2100
0.942478
$\Delta x.\Delta p $
2.082876
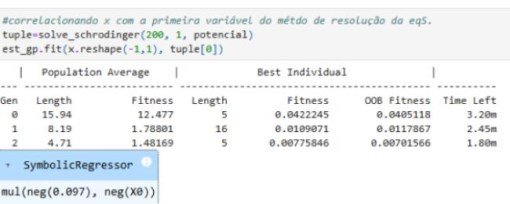
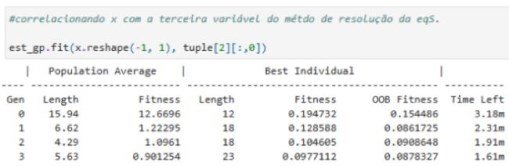
Regressão Simbólica entre os $\Delta x $ e $\Delta p $, como variáveis independentes.¶
from array import array
pr_in=[]
mul=0
co=0
for i in dp:
mul=dmp[co]*i
pr_in.append(mul)
co=co+1
pr_in
l=np.linspace(-20,20,7)
est_gp.fit(desvf,l)
| Population Average | Best Individual |
---- ------------------------- ------------------------------------------ ----------
Gen Length Fitness Length Fitness OOB Fitness Time Left
0 14.12 17.3358 61 4.58152 2.20469 3.45m
1 13.19 12.2287 63 2.01855 16.5301 2.28m
2 22.91 12.5299 68 1.48236 19.5784 3.20m
3 45.90 11.1265 67 1.35883 16.5595 3.00m
4 57.10 8.42914 74 1.2534 16.1118 2.97m
5 56.64 8.65533 103 0.940835 17.0272 2.68m
6 55.98 8.42966 74 0.897443 18.0636 3.05m
7 55.51 8.75305 89 0.915222 18.4083 2.35m
8 54.16 8.32359 57 0.83206 5.84937 2.04m
9 54.13 8.69014 59 0.601793 5.16499 1.84m
10 51.85 8.2424 59 0.601793 5.16499 1.64m
11 50.01 8.74759 70 0.566704 2.36483 1.42m
12 48.89 8.13448 63 0.433342 38.7046 1.45m
13 51.54 7.87202 75 0.439702 1.6471 1.06m
14 55.80 7.78783 74 0.409549 1.6472 59.38s
15 62.10 7.10821 63 0.414798 1.55232 56.88s
16 65.83 8.2369 79 0.343407 1.43067 37.18s
17 66.11 7.72361 78 0.387547 1.80321 24.98s
18 64.58 7.55171 78 0.274171 1.35523 13.50s
19 63.97 7.15509 77 0.328465 1.395 0.00s
sub(sub(sub(mul(neg(div(X0, X0)), add(neg(X1), div(X0, X1))), inv(add(neg(-0.046), div(-0.094, X1)))), mul(add(neg(div(add(neg(X1), add(neg(X1), neg(X1))), X0)), sin(X1)), neg(sin(X1)))), div(sin(sub(sub(sub(mul(neg(div(X0, X0)), add(neg(sub(X1, -0.041)), div(X0, X1))), inv(add(neg(-0.046), div(-0.094, X1)))), sin(0.355)), div(sin(div(-0.094, X1)), sub(X1, -0.041)))), sub(X1, -0.041)))
In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.sub(sub(sub(mul(neg(div(X0, X0)), add(neg(X1), div(X0, X1))), inv(add(neg(-0.046), div(-0.094, X1)))), mul(add(neg(div(add(neg(X1), add(neg(X1), neg(X1))), X0)), sin(X1)), neg(sin(X1)))), div(sin(sub(sub(sub(mul(neg(div(X0, X0)), add(neg(sub(X1, -0.041)), div(X0, X1))), inv(add(neg(-0.046), div(-0.094, X1)))), sin(0.355)), div(sin(div(-0.094, X1)), sub(X1, -0.041)))), sub(X1, -0.041)))
Escore:¶
print('R2:',est_gp.score(desvf,l))
next_e = sympify(str(est_gp._program), locals=converter)
y4=next_e
R2: 0.9974758366230793
Equação Proposta:¶
print(y4)
-X0/X1 + X1 + (sin(X1) + 3*X1/X0)*sin(X1) + sin(X0/X1 - X1 + 0.306590365235784 - sin(0.094/X1)/(X1 + 0.041) + 1/(0.046 - 0.094/X1))/(X1 + 0.041) - 1/(0.046 - 0.094/X1)
Regressão Simbólica entre os $\Delta x $ e $\Delta p $, como um produto entre ambas.¶
deltax=np.linspace(2.1,2.83,100)
deltap=np.linspace(0.15,0.94,100)
delta_dp=pd.DataFrame()
delta_dp['deltax']=deltax
delta_dp['deltap']=deltap
c=0
mult=[]
for i in deltax:
j=deltap[c]*i
mult.append(j)
c=c+1
c_inf=0
mult_inf=[]
mult_sup=[]
for i in mult:
if i<0.5:
mult_inf.append(i)
c_inf=c_inf+1
else:
mult_sup.append(i)
est_gp.fit(delta_dp,mult)
| Population Average | Best Individual |
---- ------------------------- ------------------------------------------ ----------
Gen Length Fitness Length Fitness OOB Fitness Time Left
0 14.12 9.75688 5 0 0 2.22m
mul(neg(X0), neg(X1))
In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.mul(neg(X0), neg(X1))
Escore:¶
print('R2:',est_gp.score(delta_dp,mult))
next_e = sympify(str(est_gp._program), locals=converter)
y5=next_e
R2: 1.0
Equação¶
print(y5)
X0*X1
As Equações Sugeridas:¶
print('As Equações Sugeridas:')
print('____________')
print('')
print('I - y1(X0) =', y1)
print('-------')
print('II - y2(X0) =', y2)
print('-------')
print('III - y3(X0,X1,X2) =', y3)
print('-------')
print('IV - y2_arr(X0) = ',y2_arr)
print('-------')
print('V - y4(X0,X1) = ', y4)
print('-------')
print('VI - y5(X0,X1) = ', y5)
print('-------')
As Equações Sugeridas:
____________
I - y1(X0) = 0.333/(0.696*X0**2 + 0.812)
-------
II - y2(X0) = -0.517*X0 + sin(X0)
-------
III - y3(X0,X1,X2) = -0.362*X1/(X0*(cos(X2) - 0.198669330795061))
-------
IV - y2_arr(X0) = sin(cos(sin(X0 - 0.773) + 0.795601620036366)*cos(1/cos(X0))/(0.130625639531083 - 2*X0**3))
-------
V - y4(X0,X1) = -X0/X1 + X1 + (sin(X1) + 3*X1/X0)*sin(X1) + sin(X0/X1 - X1 + 0.306590365235784 - sin(0.094/X1)/(X1 + 0.041) + 1/(0.046 - 0.094/X1))/(X1 + 0.041) - 1/(0.046 - 0.094/X1)
-------
VI - y5(X0,X1) = X0*X1
-------
Reinterpretando a Mecânica Quântica, por meio da
Regressão Simbólica
Ensaiando em Python
Parte 01 - Resolução do experimento do poço quadrado infinito¶
Para V(x) = 0, seleciona-se a Equação de Schroedinger, unidimensional e independente do tempo:¶
$$-\frac{\hbar^{2}}{2m}\frac{d^{2}}{dx^{2}}\psi(x)=E\psi(x)$$
Para a Equação acima, são soluções:¶
$$ \psi_n(x) = \sqrt{\frac{2}{L}} \sin\left(\frac{n\pi x}{L}\right)$$$$E_n = \frac{n^2 \pi^2 \hbar^2}{2mL^2}$$
É objetivo desta Parte 01, determinar os coeficientes c, por meio da solução seguinte integral:¶
$$c_n= \int_0^L \psi_n(x) \Psi(x,t=0) dx$$
O código da primera parte¶
#Bibliotecas
import matplotlib.animation as animation
from IPython.display import HTML
import matplotlib.pyplot as plt
import scipy.integrate as spi
import numpy as np
%matplotlib widget
%matplotlib inline
A primeira função de onda codificada é:¶
$$\Psi (x,0)=x\in\Big[0,\frac{L}{2}\Big]$$$$\Psi (x,0)=x\in\Big[\frac{L}{2},L\Big]$$
## Para a enrgia -En- da particula:
def f(x,L):
ener_p = np.sqrt(12./(L*L*L))
return (np.piecewise(x,[x<L/2.,x>=L/2.],
[lambda x: ener_p*x,
lambda x: ener_p*(L-x)]))
## Para a função de onda da particula:
def psi_n(x,n,L):
return (np.sqrt(2./L)*np.sin(n*x*np.pi/L))
O primeiro gráfico:¶
def opt_plot():
plt.minorticks_on()
plt.tick_params(axis='both',which='minor', direction = "in",
top = True,right = True, length=5,width=1,
labelsize=15)
plt.tick_params(axis='both',which='major', direction = "in",
top = True,right = True, length=8,width=1,
labelsize=15)
x_r = np.arange(0,10,0.01)
plt.figure(figsize=(8,5))
plt.plot(x_r,f(x_r,10))
plt.title(r'$f(x_{r})$')
plt.xlabel(r'$x_{r}$')
plt.ylabel(r'$f(x_{r})$')
plt.grid()
opt_plot()
plt.savefig('f(x_r).png')
Calcula-se, agora, a constante c para um n específico:¶
def int_fun(x,n,L):
return (f(x,L)*psi_n(x,n,L))
def c(n,L):
if n==0 or n%2==0:
return (0)
return (spi.quad(int_fun,0,L,args=(n,L),limit=100)[0])
A integração é feita até o ítem $c_{39}$¶
Nmax=40
L_1 = 10. # Largura do poço.
L_step = 10./100.
nl = np.array(range(Nmax))
cx = np.array([c(n,10.) for n in nl])
print(cx[0],cx[1],cx[2],cx[3],cx[4])
print(np.sum(cx*cx),cx[Nmax-1])
0.0 0.9927408002342286 0.0 -0.11030453335935887 0.0
0.9999974367055641 -0.0006526895465042513
Tendo encontrado um padrão para resolução da constante $c_{n}$, é programada a primeira versão, ainda rústica, da função de onda dependente do tempo.¶
Para tal, admitem-se $m=1$ e $\hbar=1$, onde formula-se E=c¶
$$-\frac{\hbar^{2}}{2m}\frac{d^{2}}{dx^{2}}\psi(x)=E\psi(x) \ -> -\frac{d^{}}{dx^{}}\psi(x)=\frac{2mc}{\hbar^{}}{dt}$$$$\psi(t)=e^{\frac{-i\text{ E }t}{\hbar}}$$¶
def E(n,L):
return(n*n*np.pi*np.pi/(2.*L*L))
def psi_f(x,t,L):
ener_p =np.sqrt(2/L)
out = 0
n_r = np.array(range(Nmax))
out = cx*ener_p*np.sin(x*n_r*np.pi/L)*np.exp(-1.j*E(n_r,L)*t)
s = np.sum(out)
return(s)
Gráfico da parte real da função de onda. Ainda não normalizada.¶
x_r = np.arange(0,10.,.1)
plts = []
plt.figure(figsize=(8,5))
for t in np.arange(0.,128.,12.):
y_p = [np.real(psi_f(x,t,10.)) for x in x_r]
pp = plt.plot(x_r,y_p,label="t = {}".format(t))
plt.title("Parte real da função de onda")
plt.xlabel("x")
plt.ylabel("y")
plt.legend(loc = 'best')
plt.grid(True,which='both')
plts.append(pp)
opt_plot()
plt.savefig('Parte real da função de onda.png')
SILVIO SANTOS
Seria ele, um descendente direto do Rei Davi!?


RUMO A LUGAR NENHUM.
A RESPEITO DAS TRADIÇÕES
Oh! Meu querido pai.
O DIÁRIO DE UM ERRANTE
-Gesualdo Bufalino-
“Congela-se a morte e não a vida. As células se encontram sem nenhuma coesão, uma sociedade anárquica onde não se trabalha pelo conjunto, pela vida”, adverte o médico e físico Carlos Delmonte Printes, da Universidade de São Paulo. “Além disso, por que desejar a imortalidade? É o incorrigível antropocentrismo do ser humano”
SAUDAÇÕES DE UM ERRANTE.
- Céline , Louis
O OLHAR DOS SEUS OLHOS
..., a vida é curta.
Se vivemos...
...vivemos para pisotear a cabeça dos reis.”
CARTA DE APRESENTAÇÃO
FRACASSO FINAL
OS ÚLTIMOS CINCO CAMPEÕES DE 1958.
Somente eles ainda vivem

I. Goleiros
Nílton Santos
Castilho
V. Volantes:
Gilmar
Zito
II. Laterais direitos:
VI. Meias:
Djalma Santos
Didi
De Sordi
VII. Atacantes:
III. Zagueiros:
Pelé
Bellini
Garrincha
Zózimo
Joel
Orlando
Vavá
Mauro
Dida
IV. Laterais esquerdos:
Oreco
15 de janeiro de 2023
Samuel Delmonte
30 de novembro de 2022
“...Pois vocês são o povo escolhido pelo senhor, nosso deus; entre todos os povos da terra ele escolheu vocês para serem somente dele.” - (Deuteronômio ,7, 6)
Cautela, cristãos!
Lembrem-se, o quanto antes, que dentre os ensinamentos que lhes deixaram, há ênfase em não derramar o sangue do próximo, assim como o fizeram com um judeu nazareno, chamado Jesus Cristo, de acordo com as crenças cristãs.
E, mais.
Muito mais cautela do que isso, devem, atentar-se, vocês cristãos, à verdadeira natureza das diretrizes impostas por seus deuses, para considerá-los membros da FACÇÃO CRISTÃ.
E, assim como o repetitivo e psicótico discurso do cristão, quando atribui ao seu dogma sagrado (o Evangelho), o único meio capaz de encontrar a verdade para qualquer dilema, vamos a ele.
No livro de Mateus, entre os capítulos 04 e 07, encontra-se o Sermão da Montanha, discurso proferido por JC, o judeu, mestre de todos vocês, cristãos, e cujo conteúdo profere o conjunto de condutas morais exclusivas e obrigatórias, capazes de conduzir ao status de cristandade; e aqueles que o atingissem, somente aqueles que o fizessem, seriam acolhidos pelas divindades cristãs.
Dentre essas leis morais, destacam-se:
Bem-aventurados os pobres de espírito, porque deles é o reino dos céus.
Bem-aventurados os mansos, porque eles herdarão a terra.
Bem-aventurados os misericordiosos, porque eles alcançarão misericórdia.
Bem-aventurados os pacificadores, porque eles serão chamados filhos de Deus.
Qualquer, pois, que violar um destes mandamentos, por menor que seja, e assim ensinar aos homens, será chamado o menor no reino dos céus; aquele, porém, que os cumprir e ensinar será chamado grande no reino dos céus.
Eu, porém, vos digo que não resistais ao mau; mas, se qualquer te bater na face direita,
oferece-lhe também a outra.
Eu, porém, vos digo: Amai a vossos inimigos, bendizei os que vos maldizem.
(Mateus 5, 3.5.7.9.19.39.44)
Obviamente, agregam-se à dogmática do cristianismo as leis morais do Código Mosaico, mais conhecidos como os Dez Mandamentos, cuja violação torna sumaria, a leitura dos seguintes dizeres:
“Ó, vós que entrais, abandonai toda a esperança.”
Foi a mesma frase lida por Dante Alighieri, no século XIII, inscritas na porta do inferno da sua Divina Comédia.
Tal condenação, às chamas do inferno, poderia ser, por Ele, revista, talvez, se o réu manifestasse o mais sincero arrependimento pelas insubordinações cometidas...
...além de, obviamente, voluntariar-se à submissão, da impiedosa vingança exercida por aqueles intitulados como os justos, que em nome do Estado e Sociedade, saciam seu ímpeto de ódio, sob o lema de Justiça.
Ademais, parece-me que, há um grande equívoco cometido pelos cristãos há muito. Isto é, faz, a proximadamente dois milênios, que buscam (os cristãos) divindades onde não foram chamados.
Tal fato, se fundamenta nas próprias palavras d’Ele, Yahweh, o Deus Impiedoso.
Tais discursos, encontram-se documentados na Torá (a Bíblia), e foram proferidos por Ele, a uma outra facção religiosa, para o povo de Jesus Cristo, os judeus:
O povo escolhido por Deus
Moisés disse ao povo:
— O Senhor, nosso Deus, fará com que vocês entrem na terra que vão possuir e ele mesmo expulsará
os povos que vocês enfrentarem.
O Senhor entregará esses povos nas suas mãos, e vocês os atacarão e destruirão completamente.
Não façam nenhum acordo de paz com eles, nem tenham pena deles.
Pois vocês são o povo escolhido pelo senhor, nosso deus; entre todos
os povos da terra ele escolheu vocês para serem somente dele.
(Deuteronômio 7, 1.2.6)
É justamente nesse roteiro, cujo enredo contém o deus monoteísta, o povo escolhido pelo dito cujo, portadores de uma arrogância astronômica, e por fim, todos os outros não escolhidos, portadores do ódio por quem é melhor do que eles, são eles também, com muita frequência, invejosos patológicos.
Desde os primeiros tempos, que podem ser lembrados, até este momento, sucessões infindáveis de facções religiosas, revezaram o controle do poder, numa triste epopeia da humanidade, que somente produziu perdedores, sempre aptos para iniciar uma barbárie.
E, dessa vez, sairão impunes?
Samuel Delmonte
03 de novembro de 2021
São eles como ovelhas, cujo cajado dos seus líderes, os impõe o caminho a ser trilhado, sem nenhuma possibilidade de pensar a respeito, muito menos objeção, pois, estão nas palavras do líder, as palavras d`Ele.
Deste modo, aquele que detém a liderança e é tido como um porta voz do divino, assume o status de mito, um semideus preparado para salvar os infelizes que acreditam que em algum momento serão salvos por algo.
Permite-se, portanto, as mais assombrosas e patéticas medidas governamentais, por um chefe (o Pastor do rebanho!) cujo adoecimento na própria megalomania, o faz crer ser realmente um semideus. Acredita que suas ações são justificadas na vontade de seu deus, desvirtua a administração estatal, tornando o governo dos Bolsonaristas, num Regime Louco.
Os convertidos e colaboradores deste status quo (atual situação), compartilham notórias características em comum, que, para mim, não são meras coincidências, mas sim traços genéticos (que não serão explicados aqui) que corroboram, em geral, para a formação de facções, os tais rebanhos, cujos integrantes adotam as mesmas convicções robotizadas.
Um indivíduo característico de uma facção, tal como a bolsonarista, é um típico e provável cristão, integrado num contexto econômico estável, com pouco repertorio intelectual, fato que explica os seus escassos recursos cognitivos, de tendencia a levar seus devaneios espirituais e religiosos até os mais constrangedores níveis possíveis, que cedo ou tarde, se transformam em mais uma barbárie.
Gostam de pisar e excluir os que estão abaixo, e se ajoelhar e idolatrar os que estão acima.
São forçados e doutrinados, desde suas memorias mais longínquas, a não pensar, a negar o próximo (típico do cristão) e a temer o castigo eterno. Torna-se, portanto, um humanoide, cujo termo se refere à diminuição da essência humana, do exercício de humanidade, quando abdica da sua capacidade d e reflexão a respeito da realidade.
Nietsche, na sua obra Para além do bem e do mal, identifica com maestria, os comportamentos grupais de sociedades cujos integrantes se associam a eles (os grupos) de acordo com as semelhanças que tem em comum, o que resulta na formação da moral coletiva de cada grupo. O prussiano do bigode as dividiu em duas categorias gerais: os de moral nobre e os de moral escrava, sendo todos os grupos pertencentes às classes sociais mais estáveis e dominantes economicamente. Segundo Nietsche, uma sociedade analisada de acordo com suas manifestações intergrupais, será classificada como nobre, se mediante um conflito cultural com quem é diferente, valorizar suas características fenotípicas e comportamentais, assim como a valorização da sociedade que atribui pertencimento (cultura e fenótipo). Já os de moral escrava, quando deparados com a mesma situação, valorizam o outro, despejando ódio a ele. O ódio e a moral escrava são características da sociedade brasileira, com tipicidade no eleitorado de Bolsonaro. Aliás, odiar é característica primaria do cristão.
Utilizando o eleitorado de Bolsonaro, generalizado, como referência e objeto de estudo, percebe-se com facilidade, que ódio e moral escrava são disfarces para ocultar duas outras características que integram o fenótipo dessas pessoas. De tal modo que, um típico eleitor de Bolsonaro, quando despido, mostra-se invejoso e acovardado. Não se trata de insulto, mas sim de uma hipótese genética, por se tratar de traços fenotípicos, ademais não é coincidência que dito cidadão seja também cristão e conservador.
O invejoso dissipa ódio àqueles que são melhores do que ele. A inveja, aqui é definida, como o ressentimento em não possuir algo que é do outro.
Consequentemente, entra em cena o traço fenotípico de covarde, cuja essência se dá na ausência de autorreflexão ou incapacidade de pensar por si próprio; a covardia faz daquele que dela padece, não possuir identidade ontológica individual.
Sozinhos não são nada!
Contudo, quando unidos...
...marcham como soldados, estimulados apenas pelo sistema nervoso periférico, preparam a emboscada e atacam. Confiscam o que do outro lhes gerou inveja e ódio.
É aqui que se define, com clareza, ao que me parece, a perversão.
Embora exista a classificação de perversidade, como característica de personalidade, na psicologia, não farei menção ao termo com tal rigor técnico, justamente por desconhecer a área de estudo. Entretanto, será utilizada a morfologia do vocábulo corretamente, para bom entendimento da hipótese, aqui levantada.
De tal modo que, define-se “perversidade” como “intenção de fazer o mal ou de prejudicar, maldade”.
É a vontade/desejo e, possivelmente, as vias de fato, de causar/provocar o mal ao outro, sem circunstancialmente, ganhar algo em troca. É a perversidade por perversidade, isto é, não se trata de um comportamento instaurado por alguma força maligna a priori, ou quaisquer outros delírios e devaneios semelhantes, mas sim uma característica inata, que nasce com a pessoa.
Os fatores biológicos, simplesmente desmoronam qualquer ideação afetada que atribui existência a algum Bem, tido como a priori.
Ademais, constatações, como a que está exposta acima, relativas aos traços genéticos como responsáveis pela formação do caráter, desconstroem a ideia ou necessidade de haver algum mal existente, tornando-o inverossímil.
E mais, muito mais do que isso.
Há, como condição obrigatória para que o bem exista, a também existência do seu padrão de referência, o mal. Contudo, este último já declinou pelo caminho, mas não sozinho, levou consigo o bem, que por sua vez, quem sabe, atua como efeito placebo na cabeça dos fiéis.
O típico eleitor do Bolsonaro, cristão, perverso, desespera-se com a aqui discutida, contemplação da realidade, não renuncia à sua redenção futura e, para que o bem exista e o conduza rumo à terra do nunca, dá vida ao mal.
Samuel Delmonte
29 de setembro de 2021
Da Terra Prometida, onde os adoradores d`Ele, por lá obraram, restou:
Sangue, petróleo, areia, e a santa Cruz inquisidora, reluzente, de pé, no deserto da terra santa onde já não há vida...
..., tamanha devoção, não os livrou desse miserável fim...
...ninguém, por eles, interveio.
E atualmente, qual é o futuro que fomentamos às nossas crianças?!
Parece, que nada impedirá, que nossos filhos e filhas, sejam testemunhas de um apocalipse lento e cruel, assombrado por,
Fanáticos religiosos, políticos psicopatas, e uma polícia, que além de corrupta, é assassina e massacra as populações mais desamparadas.
E, por último. Esqueçam!
Não haverá redenção nenhuma. Ele não virá por ninguém. Estamos todos entregues à própria sorte.
De duas, uma:
Ou, Ele, de fato não existe.
Ou, estavam certos os primeiros, e Yahweh, escolheu somente o povo de Abraão.
Samuel Delmonte
02 de agosto de 2021
Não há o que temer, a alma é finita e não há vida após a morte. - Epicuro
O cristianismo foi, até o momento, a maior desgraça da humanidade, por ter desprezado o Corpo. - Friedrich Nietzsche`
Não há melhor forma de começar as argumentações conclusivas deste ensaio, senão que, por meio das palavras Dele:
...certa vez, Yahweh ordenou ao seu povo, a destruição daqueles que Ele não escolheu...
...o Deus deles, os escolhidos, manifestou a sua vontade com as seguintes palavras:
BÍBLIA HEBRAICA
Livro Quinto: Deuteronômio
Capítulo 07
v.01- O Senhor, nosso Deus, fará com que vocês entrem na terra que vão possuir e ele mesmo expulsará os p ovos que vocês enfrentarem...
v.02- O Senhor entregará esses povos nas suas mãos, e vocês os atacarão e destruirão completamente. Não façam nenhum acordo de paz com eles nem tenham pena deles.
v.03- Não se casem com essa gente, nem vocês, nem os seus filhos ou as suas filhas,
v.04- pois esses povos farão com que os seus filhos rejeitem a Deus e adorem outros deuses. Aí o Senhor Deus ficará irado com vocês e os destruirá de uma vez.
v.05- Portanto, derrubem os altares desses povos, quebrem as colunas do deus Baal, cortem os postes da deusa Aserá e queimem todas as imagens.
v.06- v.06-Pois vocês são o povo escolhido pelo Senhor, nosso Deus; entre todos os povos da terra ele escolheu vocês para serem somente dele.
A passagem bíblica acima, enfatiza a aliança feita por Deus com o povo judeu, exposto com as próprias palavras Dele. Aliás, são eles, os hebreus, os criadores da infame representação de um deus único, cujo monoteísmo, sempre dogmático, cresceu, no decurso do tempo, como um câncer em fase de metástase, que assombra a humanidade até os dias atuais.
Deuteronômio é o quinto livro da bíblia judaica. Os cinco primeiros, são conhecidos também, como a Torá, e moldaram a idolatria monoteísta através de um deus cruel, impiedoso e vingativo; ademais, mostra-se (Yahweh) tirano ao exigir freneticamente adoração a si próprio, em troca da graça futura do seu povo.
A epopeia da bíblia hebraica, assemelha-se a um conto cujo gênero é híbrido, iniciando como uma estória de terror, por desenvolver um enredo da relação dos escolhidos com Ele, que é, a olhos vistos, simplesmente patológica, sem cura, e vai deixando, por onde quer passe, barbáries sem fim. Mas, no final das contas, o conto termina, já no gênero infantil, “cumprindo sua promessa” de que, enfim, todos serão felizes para sempre, saltitando na Terra do Nunca.
O personagem original do Deus único, retratado na bíblia hebraica, não é bondoso e misericordioso na sua completude, pois mata aos montes, sem nenhuma piedade, é cruel o bastante para dizimar um povo, não deixar ninguém vivo, além de aterrizar os seus escolhidos para que façam o serviço sujo, sem retroceder. Ele é irônico, e faz diferença com as pessoas, o Rei Davi, citando um exemplo, era o seu preferido.
Por essas caraterísticas, houve quem, durante o passar do tempo, lhe conferisse a Ele o status de mal. No livro de Jó, há algumas referências a esta possibilidade, sobretudo nas angústias de Jó, quando já não compreende o sentido das provações que lhe são impostas. Há, também, um diálogo que, grosso modo, diz:
- Reze para não ser escolhido por Ele!
Até aqui, percebe-se, através do conteúdo bíblico, a construção, feita pelos hebreus, do primeiro personagem divino associado à uma facção religiosa, e apenas uma. De tal modo que, toda a impetuosidade disparada por Yahweh (o tal Deus deles) a todos que não sejam escolhidos, inclui também os cristãos.
Não há nada transcendente ou metafisico que derrube o próprio argumento que os crentes, em geral, usam para desesperadamente mendigar o status de filho bastardo Dele. Este argumento se refere às palavras Dele, escritas no livro que lhe atribuem ter explanado suas leis. A Bíblia. E Ele foi bem claro na sua preferência, contidos nos versículos acima.
Enfim, concluirei este conjunto de ensaios com um último argumento, construído com as informações expostas nos parágrafos acima...
..., mas desta vez, considerarei a absurda e infantil convicção de que Ele existe (refiro-me ao deus do velho testamento) ....
... e se assim fosse, certamente todos os cristãos não estariam na lista dos escolhidos, e tampouco elegíveis para a redenção futura...
...tanto é que além de ninguém aparecer para a dita salvação, a pandemia, em toda a sua perigosa magnitude evidência, de acordo com as funções que atribuem a Deus, quem foi escolhido e quem não foi...
Deste modo, a epidemia global, seria um daqueles clássicos momentos que o crente convicto espera pela salvação Dele, em troca da sua devoção...
...contudo, não foi o que aconteceu, nem foi verificada nenhuma salvação aos cristãos, pelo contrário, países de maioria cristã, inclusive os europeus, foram as nações mais afetadas pelo corona vírus, com maiores números de mortes...
Diferente dos países a leste, que foram os primeiros a se recuperarem, como Israel, por exemplo, pais cujo 80% da população se autointitula como os “ESCOLHIDOS”.
Mal sabem eles que ninguém superará o grande e inerente fracasso final... ...e nesta hora da verdade, que chegará para todos, se alguém sair vitorioso, ele será algum Anjo Caído.
Samuel Delmonte
27 de maio de 2021
A natureza não é cruel, apenas implacavelmente indiferente. Esta é uma das lições mais duras que os humanos têm de aprender - Richard Dawkins
Decidi, por razões de dívida moral com meus antepassados, retomar a pesquisa genealógica iniciada pela minha tia avó, Rosalina Delmonte e meu pai, Carlos Delmonte, ambos falecidos e cujos esforços para delinear a linhagem de nossos ascendentes Delmonte, além de traçar a rota de perambulação deles, do inicio da idade moderna, até sua imigração para o Brasil, em 1895, geraram poucos frutos.
Iniciei do zero!
Minha ascendência conhecida, está quase toda morta. Ademais, minha prioridade, são os Delmonte, a quem intuo possuir, a maior parte do meu genoma adquirido. Contudo, é fato que meus familiares paternos morrem demasiadamente cedo, sem deixar muitos rastros. Não conheci quase ninguém!
Há que possuir entusiasmo!
Pouco a pouco, garimpo evidencias que se tornam pistas promissoras, nesta solitária busca pelas minhas origens...
...e mais, mais importante do que isso....
....sinto o dever de reverenciar meus antepassados mortos; manter viva a lembrança de quem algum dia eles foram; por onde passaram, de onde fugiram; em que lugar triunfaram, em qual solo derramaram nosso sangue.
Gostaria, se assim fosse possível, dividir com todos eles, o amargo sabor das suas lagrimas!
Das minhas muitas ironias, uma delas parece ter fundamento genético hereditário; isto é, quando digo que deveria ter nascido nos alpes, em razão do meu desconforto com o calor e as baixas altitudes (baixa pressão arterial), podem, tranquilamente serem consequências da minha origem (superior a 50%) do norte da Itália, na região alpina, que faz fronteira com a Suíça. E por ambas as vias (paterna e materna), são apenas três gerações, que me separam dos Alpes.
Devo continuar, sem desistir, pois eu sei bem que é da agonia que sairá meu triunfo.
Abaixo, homenageio os Delmonte holandeses, os quais encontrei indícios de parentesco com eles. Logo após, segue minha arvore genealógica em plena construção:
PESQUISA FEITA EM HOMENAGEM AOS DELMONTE QUE PADECERAM NOS CAMPOS DE CONCENTRAÇÃO DA POLÔNIA
DELMONTE – MORTOS NO HOLOCAUSTO
| NOME | NASCIMENTO | MORTE | CAMPO |
|---|---|---|---|
| Salomon Delmonte | 1916, Amsterdam | 11/8/1942 | Auschwitz |
| Rosette Swart (nasc. Delmonte) | 1878, Amsterdamg | 31/8/1942 | Auschwitz |
| Esther Pezaro (nasc. Delmonte) | 1891, Amsterdam | 14/9/1942 | Auschwitz |
| Jozeph Delmonte | 1922, Amsterdam | 18/9/1942 | Auschwitz |
| David Delmonte | 1913, Amsterdam | 30/9/1942 | Auschwitz |
| Nlida de Hoop (nasc. Delmonte) | 1883, Amsterdam | 5/10/1942 | Auschwitz |
| Isaäc Delmonte | 1887, Amsterdam | 21/10/1942 | Auschwitz |
| Sara Mendels (nasc. Delmonte) | 1861, Amsterdam | 1/2/1943 | Auschwitz |
| Mozes Delmonte | 12/2/1943 | Auschwitz | |
| Gracia Delmonte | 1880, Amsterdam | 20/3/1943 | Sobibor |
| Maurits Delmonte | 1881, Amsterdam | 20/3/1943 | Sobibor |
| Salomon Delmonte | 1879, Amsterdam | 2/4/1943 | Sobibor |
| Sara K. de Vries (nasc, Delmonte) | 1884, Amsterdam | 14/5/1943 | Sobibor |
| Rosette Blitz (nasc. Delmonte) | 1867, Amsterdam | 21/5/ 1943 | Sobibor |
| Reine Delmonte | 1924, Amsterdam | 28/5/1943 | Sobibor |
| Elsje Delmonte | 1927, Amsterdam | 11/6/1943 | Sobibor |
| Jacob Delmonte | 1895, Amsterdam | 11/6/1943 | Sobibor |
| Maurice Delmonte | 1928, Amsterdam | 11/6/1943 | Sobibor |
| Roosje Pach (nasc. Delmonte) | 1893, Amsterdam | 2/7/1943 | Sobibor |
| Rachel Monas (nasc. Delmonte) | 1857, Amsterdam | 24/9/1943 | Auschwitz |
| Benjamin Delmonte | 1865, Amsterdam | 18/3/1944 | Bergen-Belsen |
| Jacob Delmonte | 1907, Amsterdam | 31/3/1944 | Auschwitz |
| Paula Stoppelman (nasc. Delmonte) | 1896, Altona | 6/11/1944 | Bergen Belsen |
30 de janeiro de 2021
MUITO SEMELHANTE AO ROTEIRO DE UM FILME PORNÔ GAY...
...a cúpula do governo apresenta:
É curioso, e, desta vez, não acredito que seja mera coincidência.
Mas, porque todo oficial de alta patente das forças armadas brasileiras geralmente: não passa do 1,70 m de altura, possuem abdome saliente, os cabelos ruins para pentear, simetria caricaturada do conjunto cabeça – tórax – membros, e nenhum indício de que algum dia foram atléticos?
Ainda não desenvolvi uma hipótese razoável para tal. Entretanto, tenho palpites, que acredito, serem promissores
Um deles recai sobre um possível bullying traumático na idade jovem, que terminou sendo um dos fatores determinantes para a maioria das tomadas decisões subsequentes.
Outro palpite diz respeito há anos de torturas dogmáticas familiares, assombradas por inúmeras figuras autoritárias que impõem regimes autoritários para tudo e para todos.
E um terceiro, que é o assunto desse ensaio, desconfia que exista um frequente complexo de inferioridade entre pessoas assimiladas a grupos sociais conservadores, fanáticos às facções cristãs e ostentador de uma série de figuras autoritárias masculinas.
Parece-me, que à medida que adquiro maturidade e repertorio, aproximo-me, por ironia, das ideias de Freud a respeito da sexualidade reprimida, que a meu ver é o caso desse contexto, que aqui, é discursado.
Portanto, é muito comum que simpatizantes de doutrinas conservadoras, que aliás de supremacistas não tem é nada, possuam dúvidas, guardadas `a sete chaves, sobre suas masculinidades.
Haja vista que indivíduos que sempre estão com o boilola na boca e adorando imagens de poder masculinas, tendo como uma delas um moribundo seminu e pendurado numa cruz, certamente reprimem seu verdadeiro eu.
E, mais, muito mais do que isso.
Agrega-se ao já relatado, o ato, também frequente, de vociferar desesperadamente aos quatro ventos o quão vil e másculo é si próprio, fazendo-o prometer ao próximo, com base em ameaças, reprimendas de ordem física, que vão desde socos e pontapés, passando, aos disparos de pistolas e fuzis até chegar na ira do seu deus, um verdadeiro Demiurgo (O Deus Mau – Concepção dos gnósticos cristãos a respeito da essência má de deus)!
Tais promessas nunca, eu disse nunca, se consolidam nas vias de fato.
Há um ditado popular que diz o seguinte:
Quem muito macho diz ser, esconde algo oposto a isso dentro de si.
Inclusive, tal citação foi utilizada pelo meu pai algumas vezes, nos seus ensinamentos dirigidos a mim. Lembro-me, como se fora ontem, suas palavras, que eram algo assim:
Samuel, você como homem deve se impor, de modo que, não fuja da briga se ela é inevitável; contudo, a verdadeira hombridade é conquistada através do intelecto, e é assim que nós, os Delmonte, procuramos agir.
E, antes de encerrar, lhes digo uma última consideração aos inúmeros covardes e estrupidos dos quais esse ensaio trata, que assim segue:
Embora, eu já não acredite, há muito, nas flores vencendo o canhão; é do lado delas que continuarei a batalha.
30 de outubro de 2020
“Tenho de proclamar a minha incredulidade. Para mim não há nada de mais elevado que a ideia da inexistência de Deus. O homem inventou Deus para poder viver sem se matar."- Fiódor Dostoiévski
“Eu vejo o que está certo e aprovo, mas faço o que está errado.” – Alex Delarge (personagem protagonista do filme Laranja Mecânica)
“Se Deus não existe, então tudo é possível e permitido!?” Fiódor Dostoiévski
Com essa indagação de Dostoievski foi encerrada a parte I deste ensaio.
E como já profetizado, iniciaremos esta segunda parte com a resposta monológica daquele que pergunta e, é para mim, a reflexão mais satisfatória ao paradoxo tautológico entre o bem e o mal.
Para Dostoiévski, a maioria das pessoas são incapazes de pensar por si só, e, portanto, inábeis para decidir a condução das suas ações através de um conjunto de valores próprio, filtrado por si mesmo...
...de tal modo que o grande romancista russo lamenta a necessidade de existirem conceitos infames de autoridades tais como deuses, polícia e afins, para imporem a ordem por meio do medo, evitando, dessa forma, que tudo seja possível e permitido.
Em contrapartida, Fiódor acredita ser totalmente possível que um virtuoso, aquele que pensa com sua própria cabeça, possa, na sua introspecção, optar pelo bem (criado por convenção social), tendo ciência do que é mal. Eureka!!!
E a Laranja Mecânica! Como se encaixa aqui nesse contexto?
Em primeiro lugar, exalto a magnifica obra brilhantemente adaptada para o cinema pelo genial Stanley Kubrick, que é, quase sempre mal interpretada.
A obra foi escrita por Anthony Burgess, que criou, como estrutura contextual, um dialeto baseado em gírias britânicas com algo de russo, o que torna difícil compreender a ideia-chave da obra não tendo a língua inglesa como nativa; acreditem! Digo por experiencia...
Sabe-se que o filme trata de violência...
...contudo, ele (o filme) se refere a um tipo específico de ato violento, que simplesmente aterroriza a maioria das pessoas de tal modo que elas negam a possibilidade de ela existir.
A violência assume, aqui nesse caso, o status de perversidade, cujo temerário autor é conhecido como o perverso, o vicioso...
...embora sejam termos pouco utilizados no português, são eles significativos para a psicologia forense, por se tratar das características de um comportamento, nasce exclusivamente do indivíduo.
Serei, a partir de agora, mais específico:
- O enredo do filme ironiza a infantil ideia de que existem leis morais universais e que são regidas por entidades místicas preocupadas conosco.
O argumento do Laranja Mecânica é sólido, afinal as personagens manifestam a perversidade pura, ou perversidade originada nela própria...
...., grosso modo, é a violência gratuita, sem ambicionar nada em troca, que não tem origem em algum mal que se possa classificar:
- Não se origina de um incontrolável desejo sádico. – Tampouco se origina na apropriação (roubos, furtos) de bens de valor. – Não são oferendas ao demônio. foi para mim, o que melhor entendeu a dura realidade discutida acima, além de encontrar uma alternativa bastante satisfatória para ela...
- São na verdade traços do comportamento humano, que nós enxergamos como hediondos, e os são, mas surgem da incontingência, do aleatório milhões de anos em que complexos genéticos são submetidos ao crossing-over da meiose e eventuais mutações.
É ele, o gene, o verdadeiro galã da história; é ele que protagoniza, há 4,5 bilhões de anos, a história da vida.
Nota-se que há muita violência no mundo real que simplesmente não é culpa de algum mal concreto, que seja preestabelecido, eterno; não há culpados, com exceção do autor, cujo ato é motivado apenas pelos seus traços humanos.
Como se observa a inexistência do mal como coisa em si, desmorona a possibilidade do seu dependente, o bem, existir.
E finalmente, analisamos o argumento observando a pandemia.
O novo Coronavirus surge do aleatório, do acúmulo de especificação que cadeias carbônicas adquirem nos milhões de anos citados acima....
.... que, além disso, não são fenômenos portadores de consciência.
Em síntese, o vírus e as suas terríveis consequências não são culpa de ninguém, embora ridículos conspiradores, doentes incuráveis da ignorância, acusem os chineses de criarem o vírus, sendo que por ironia, eles, os chineses, veem fazendo muito no combate ao covid-19, muito mais do qualquer deus.
“Relaxem, pois a vitória sempre será do Anjo Caído... ...o corajoso luta a batalha, mesmo ciente do seu fracasso final... ...o covarde, tendo o cristão como o seu mais fiel representante, se amedronta e se esconde atrás das mais delirantes e patéticas figuras autoritárias possíveis.” - Samuel Delmonte
21 de setembro de 2020
“Que lamentável condição do homem! Ter que ser domado pelo medo ao castigo e pela esperança de uma recompensa depois da morte.” – Albert Einstein
“O importante é a escolha moral. O mal tem que existir junto com o bem, para que a escolha moral possa funcionar. A vida é sustentada pela oposição das entidades morais.” – Alex Delarge (personagem protagonista do filme Laranja Mecânica)
Somente existirá o bem se, em contrapartida houver o mal como seu antagonista e referência do que é imoral. É uma dependência recíproca e necessária.
Existe, portanto, desde que o mundo é mundo, a necessidade de dogmatizar leis morais que determinem o que é bom, e o que é mal...
...e sempre, eu disse sempre há um desespero coletivo da grande maioria de idiotas que existem por aí em rotular acontecimentos como consequência das forças do bem, ou do mal.
Encontra-se, dessa forma, um sentido de ser e existir a tudo o que acontece a nossa volta...
...nada pode surgir do aleatório, do nada...
...e até mesmo o que se considera vindo do mal é altamente justificável como uma relação de causa e efeito; vejamos:
- O ladrão se beneficia do objeto roubado; - O corruptor e o corrompido obtém vantagens mútuas; - O assassino em série mata com o objetivo de saciar seus desejos sádicos, e por aí vai...
...é claro que, na frente oposta, existe um poderoso ópio mais conhecido como justiça, que condena os atos imorais, como os citados acima, e justifica o bem triunfando sobre o mal.
Contudo, não posso entender como são tão poucas as pessoas que podem enxergar o obvio, e perceber, sem muito raciocínio, que os preceitos éticos e morais são uma mera criação humana, que inclusive, percebe-se por aí, diferentes dogmas, rituais, facções religiosas, que são manifestações morais de grupos que são contemporâneos e situam próximos uns dos outros; fato este, que impossibilita a ideia ridícula de que existem, a priori, entidades boas ou más.
Portanto, não há de existir manifestações más, ou algo parecido, que influencie ou atue em fenômenos naturais, tampouco nas ações humanas...
...de modo, que se não há o mal por si só e a priori, deixa de fazer sentido existir o bem com as mesmas condições.
Concluiu-se até aqui, que conceitos como o bem e o mal são criações humanas; ademais, todo o restante da natureza é indiferente a eles, afinal não existem como coisa em si...
...além disso, tampouco existe um sentido predeterminado ao mundo a nossa volta, que exista como coisa em si, pois simplesmente a realidade não se comporta dessa maneira...
...somos nós que damos sentido às coisas para que nossas existências sejam o menos sofridas e desprezíveis possível.
Enquanto os fracos esperarem a salvação eterna e conduzirem suas ações em busca disso, criam um contexto psicológico perverso, cuja vitória final é do Anjo Caído, encenado pelas massas.
Na parte II, usarei como exemplo de inexistência de preceitos morais que sejam predeterminados antes do pensamento humano (como coisa em si e a priori das ideias humanas), o célebre filme – Laranja Mecânica -, dirigido por Stanley Kubrick, e logo em seguida, fecharemos com chave de ouro esta ideia, utilizando como observação um claro e não excelente exemplo, do aqui vem sendo exposto:
- A pandemia do novo Coronavírus.
Não poderia encerrar essa primeira parte, sem antes citar Fiódor Dostoievski, um dos meus heróis, que apesar de não ter sido filosofo, foi para mim, o que melhor entendeu a dura realidade discutida acima, além de encontrar uma alternativa bastante satisfatória para ela...
29 de julho de 2020
“Os encantos dessa sublime ciência se revelam apenas àqueles que tem coragem de irem a fundo nela.”. - Carl Friedrich Gauss
“A primeira lei da natureza é a tolerância – já que temos todos uma porção de erros e fraqueza.” - Voltaire
Neste fascículo busco elucidar como a métrica de construção deste ensaio, ou a hipótese que está inserida nele, é significativamente diferente de crenças dogmáticas, normas preestabelecidas e até mesmo de ideologias que sempre fracassam quando postas em prática.
Não obstante, sigo convencido de que o cristianismo é uma facção cujos seguidores, os cristãos, são em geral, indivíduos inúteis: com déficit de inteligência, predisposição à barbárie e uma inveja única às qualidades do outro.
De qualquer forma, o princípio de que carrego comigo desde os tempos da pré-adolescência, baseia-se no empirismo; além, é claro, do repertorio de leituras que acúmulo nestes anos.
Além disso, sou um profundo admirador do modelo científico rigoroso reducionista; aquele cujos passos seguem a seguinte ordem: hipótese, observação, quantificação e teste.
Na quantificação, preciso deixar margem à dúvida; senão, minha hipótese torna-se uma pista falsa.
Faz-me companhia agora, Gauss; o príncipe da matemática! De cuja curva normal sempre é infalível quando deixamos 5% para o erro....
...e, é desta pequena imperfeição que contradigo a mim mesmo e admito aqui, quais foram as duas únicas pessoas que realmente demonstraram atos de cristandade para comigo...
...fato do qual me impressionou absolutamente!
Essas duas moças na foto ao lado são a Bruna (à direita), e a Fernanda (à esquerda) ...
...e foram elas que me surpreenderam ao demonstrarem afeto e preocupação comigo, sem realmente querer algo em troca que não seja a minha amizade...
...elas realmente se importam.
Ademais, elas, de antemão, já sabiam o teor das minhas opiniões e o desprezo que tenho por aquele que crê.
Aliado à surpreendente prática do sermão da montanha, são elas inteligentes, agradáveis, interessantes, com todo o respeito...
...inclusive, elas são membros de uma mesma família cujos integrantes que conheci possuem características semelhantes entre si, ` o que contradiz o perfil que tenho do cristão em geral, exceto pela prática genuína das suas crenças.
Não poderia eu aqui, deixar de homenageá-las om a minha mais sincera gratidão por havê-las conhecido....
Agradeço a vocês também por afastarem-me da convicção, semeando a dúvida que alimenta meu ceticismo; que por sua vez possibilita, segundo Voltaire (o homem que trouxe a luz!), a aparição da tolerância.
16 de julho de 2020
“O ódio é a vingança do covarde.” - George Bernard Shawo
“Parece-me que jamais haverá coragem naquele ou naqueles que idolatram líderes; restará a eles, portanto, covardia.” - Eu mesmo.
E o golpe, quando será?
E as suas amadas armas, cristãos (os homens de bem), ....
...não as empunharão?
E por onde marcham os orgulhosos pelotões das tropas bolsonaristas?
Não estariam demorando para impor a ordem nas ruas, todos aqueles que urraram por aí suas convicções de ódio ao próximo...
...não estavam tão sedentos por instaurar uma soberania nacionalista cristã através da força?
Ou na verdade, toda essa elite, que fala muito e faz pouco, assemelha-se muito mais aos comediantes da imagem ao lado, do que aos 300 espartanos das históricas guerras médicas da antiguidade.
Já que citei os formidáveis antigos da Grécia, continuo com a sempre bem vinda companhia deles, afirmando que um moralista sempre terá ausente no seu caráter a coragem, também conhecida como a mãe das virtudes; alguns filósofos gregos utilizam o termo virtude com o significado direto de coragem.
Ademais, um dogmático, não satisfeito com a sua falta de coragem, recorre amedrontado a Platão, e, por conseguinte, cria um perverso ideal platônico de coragem sustentado por um conto de fadas infestado de personagens bizarros, que vão desde:
... um moribundo com fisionomia ariana pendurado numa cruz; um deus, também descrito como ariano na arte renascentista, que dizem ser bom, mas o mundo que criou não. Patético!
Neste delirante conto, existe também a crença de que militares, milicianos e generais resolverão problemas de ordem cultural, sendo que eles estão muito mais preocupados em reafirmar as suas masculinidades aos outros e, curiosamente eles nunca passam de 1,65 metros de altura.
Apenas um covarde refutaria como existente uma realidade medonha, tal qual descrevi acima!
Aliás, nossa elite tupiniquim, decadente e inautêntica, deseja incontrolavelmente ser reconhecida como supremacista cristã...
...oh! infame status...
...contudo, não nos esqueçamos que nossas origens europeias são, em geral, latinas, com forte descendência portuguesa, espanhola e italiana, que no período imigratório, compreendido entre a segunda metade do século XIX e a primeira do século XX, já eram a escória da Europa ocidental...
...e, fugiram da fome e da sede dos seus países para substituir a escravidão negra no Brasil...
...muitos deles eram analfabetos e desdentados.
Agora, novamente faço a pergunta?
-Virão para cima, ou não?
Estou doidinho para morrer defendendo minha intuição que carrego desde a infância; intuição essa que eu descreveria da seguinte forma:
- A união de indivíduos, cuja ignorância metastática e incurável assombra o mundo há muito. Esta facção tão hábil no retrocesso humano é o cristianismo. –
Mas, voltando ao assunto deste fascículo 03, digo sem temor que todos aqueles que buscam expressar desesperadamente sua masculinidade e são incapazes de agir por si próprios, fogem assustados de algo enrustido nos seus interiores...
...são, portanto, uns bundas-moles!
Já dizia o velho ditado:
“Quem é homem não precisa sair por aí se afirmando como tal.”
De modo que, terminei encontrando as respostas às minhas indagações iniciais nos próprios argumentos que utilizei...
...e sem muito esforço encerro com a seguinte conclusão:
- Esse rebanho de pessoas, que deliram acordadas com a bíblia numa mão, e um fuzil na outra, não passam de um bando de covardes e bunda-moles que não farão nada, afinal, sempre se escondem atrás de um crucifixo ou de um bobo da corte como o Bolsonaro que logo, logo estará sem nenhum seguidor quando já não tiver mais poder ao alcance das suas mãos. -
E, sem mais o que dizer, encerro esta terceira parte com as palavras de um sábio, cuja coragem assustadora é para mim, outro grande herói:
“Todo pobre-diabo que não tem nada no mundo do que possa se orgulhar escolhe a nação a que pertence como último recurso para sentir orgulho: desse modo, ele se restabelece, sente-se grato e pronto para defender com unhas e dentes todos os erros e absurdos próprios dessa nação.” - Arthur Schopenhauer
04 de julho de 2020
“O cristianismo tornou a crença sem reflexão em uma sabedoria, a hipocrisia humana em conselho divino, a corrupção
da lei natural em piedade religiosa, o estudo em loucura, a honra em riqueza, a dignidade em elegância, a prudência
na malícia, a traição na sabedoria e a justiça na tirania.”
Giordano Bruno
Um ser humano somente fará a diferença, se e somente se, ele for portador da arte de pensar com a própria cabeça; isto é, apenas aqueles que são capazes de questionar e refletir a respeito de dogmas e preceitos morais pré-estabelecidos, poderão, quem sabe, fazer o bem.
Grosso modo, não acredite cegamente no que dizem por aí, simplesmente. Questione, reflita e tire suas próprias conclusões.
Sempre fui atraído pelo Punk justamente porque seus adeptos, são, na sua maioria, capazes de enxergar a realidade com olhos não tão entorpecidos; e como o que vemos soa desesperador, nos entorpecemos depois. (risos)... `
...uma das pouquíssimas verdades que a vida me mostrou é brilhantemente cantada por uma das célebres bandas do punk rock paulistano no trecho citado abaixo:
- “...não acredites nos seus líderes, pois todos eles irão te trair...”
(Anarquia Oi - Garotos Podres) –
Estou a cada dia mais convencido de que nossas origens como uma espécie animal são muito mais relevantes na implicação das crenças que teremos e nas facções que pertenceremos, do que qualquer estímulo ou influência externas.
Aproximo-me, agora, da essência da hipótese que é a razão da minha pesquisa que, aqui exponho nestas tortas linhas...
...e que hipótese é essa?
Pois bem, tentarei explicar ao longo dos fascículos.
Até esse momento posso adiantar que tal hipótese defende a tese de que a verdadeira essência de alguém será conhecida através dos seus vícios, hábitos e pelas suas crenças, cujas manifestações se darão dentro de grupos e facções que reluzirão a mesma essência...
...além disso, parece-me que não é uma mera opção ou escolha nossas crenças e hábitos, são na verdade, condições comandadas por sequencias genéticas.
Portanto um grupo ou uma seita atraem pessoas com características biológicas semelhantes...
...e o cristão, na sua maioria, possui claramente as características mais limitadoras que um individuo pode possuir, tornando-o imprestável, em geral, para fazer a diferença. O que não deveria ser um problema, afinal qualquer ser humano é digno de ter acesso às mesmas coisas...
...não se esqueçam que sou um anarquista.
No entanto o cristianismo constitui o pior dos canceres, afinal ele tem o poder de manipular um rebanho gigantesco com base numa incurável ignorância, pois o cristão, nada mais é do que um indivíduo com:
1- Limitados recursos intelectuais;
2- Possuidor da famosa moral do escravo de Nietzsche (a moral do escravo é aquela que a identidade pessoal da crença é formada naquilo que o outro tem e lhe falta – é a inveja, basicamente.
3- Apresenta também, a covardia patológica, ou seja: a inexplicável necessidade de obedecer a um líder, traduz esta característica (O Bolsonaro é um bom exemplo).
Este portanto, é o verdadeiro cristão...
...e é disto que tratará este ensaio.
...e o farei sem puder, afinal se por acaso eu também for um covarde, lutarei ao menos para deixar sê-lo.
16 de junho de 2020
“Não há nada mais repugnante do que adorar um moribundo pendurado numa cruz.”
Finalmente venci a covardia e aqui começo meu manifesto, que é fruto da mais genuína e sincera forma que vejo o mundo.
É também minha oportunidade de homenagear meus corajosos heróis. Todos eles são, é claro, hereges, deuses de si próprio. Oh! Corajosos de alma!
Procurarei demonstrar, nesta coleção de fascículos, que as malditas convicções atraem rebanhos humanos com características muito semelhantes, todos desprovidos das mais básicas necessidades humanas que os classifiquem como civilizados, tais como refletir ou pensar por si próprios.
Meu foco aqui neste ensaio, é demonstrar como o cristianismo num câncer metastático que necrosa o mundo há muito...
... discursarei sem temor, cada vez mais convencido de que o cristão é o retrato da imperfeição da natureza, mesmo sendo elegante, ela...
...a Natureza Elegante, decretou, sua certa morte precoce, quando sua variabilidade randômica fez surgir a religião.
O tcheco Franz Kafka, profetiza com sua impiedosa simplicidade, mais ou menos assim:
“Definitivamente não haverá salvação nenhuma.”
...e desmorona o antigo delírio dos fanáticos.
Não poderia encerrar esta introdução sem antes refutar minhas breves considerações, através do discurso do mestre dos mestres...
Albert Einstein:
A religião serve para o homem`...
...assim como a viseira serve para o cavalo.
Jamais poderá admitir, cristão...
..., que alguém mais inteligente e estudioso que tu, questione tuas crenças...
..., porque sabes que toda a sua vida está apoiada em mentiras incuráveis...
...e que um simples sopro é suficiente para reduzir-te a um espectro acabado.
Quando ensinaras teus filhos a questionar a vida...
..., os dogmas, as mentiras e as farsas que o estado e a educação contemporânea lhes injetam nas veias à força?
Eu prefiro uma criança rebelde, critica, criativa e autônoma...
...em lugar dessas pobres criaturas domesticadas, massificadas e servis que povoam tuas escolas
15 de dezembro de 2019
Eu sei muito bem que meu reflexo no espelho é a semelhança para com o mal; assim como, ao olhar para outra pessoa, vejo o mesmo mal.
Alguns dos erros que cometi, são para mim, ulceras das quais carregarei comigo até o dia da verdade, dia que me depararei com o absoluto vazio.
Não honrei meu pai, erro que já é tarde para reparar e cujo arrependimento continuará estando até o invariável fim.
Contudo, é esse arrependimento que fortalece minhas aspirações, não para modificar o que já foi, mas sim, o que está por vir.
Dessa maneira, meu pai, a pendência que, todavia possuo contigo é, transmitir seu material genético e, sobretudo, sua memória a um novo hospedeiro que, também carrega consigo, nossa origem e nosso nome.
Portanto, querido pai, não se preocupe, afinal, não descansarei até que sua netinha saiba quem realmente você, algum dia foi, e, continuará sendo, na memória daqueles que, carregam algo de ti.
São também, frutos do arrependimento, os meus esforços para construir o dia de amanhã, diferente daquilo que há tempos fiz e, retribuir, mesmo que infimamente, tudo aquilo que, a mim, foi feito por ela, a minha mãe.
Ademais, minha mãe, os seus esforços para me manter vivo, impossibilitam que as palavras traduzam semelhante ato!
Além disso, foi você, minha mãe, a única que esteve presente nos piores momentos. Oh! Sim! Nos piores!
Não me atreverei a chegar até o inerente descanso final, sem antes consolar os seus próprios arrependimentos, minha mãe; vou estar presente quando necessites.
Sem mais o que dizer.
Ocupo-me de, construir o pai que tem por direito, Victória, a minha filha e, construir o filho que tem o dever de conceder seu ombro às tormentas daquela que realmente importa, a sua mãe.
É disso que trata o meu arrependimento...
14 de dezembro de 2019
“O nosso “amor pelo próximo” não será o desejo imperioso de uma nova propriedade? E não sucede o mesmo com nosso amor pela ciência, pela verdade? E, mais geralmente, como todos os desejos de novidade? Cansamo-nos pouco a pouco do antigo, do que possuímos com certeza, temos ainda necessidade de estender as mãos; mesmo a mais bela paisagem, quando vivemos diante dela mais de três meses, deixa de nos poder agradar, qualquer margem distante nos atrai mais: geralmente uma reduz-se com o uso. O prazer que tiramos a nós próprios procura manter-se, transformando sempre qualquer nova coisa em nós próprios; é precisamente a isso que se chama possuir.
Cansar-se de uma posse é cansar-se de si próprio. (Pode-se também sofrer com o excesso; à necessidade de deitar fora pode assim atribuir-se o nome lisonjeiro de “amor”.) Quando vemos sofrer uma pessoa, aproveitamos de bom grado essa ocasião que se oferece de nos apoderarmos dela; é o que faz o homem caridoso, o indivíduo complacente; chama também “amor” a este desejo de uma nova posse que despertou na sua alma e tem prazer nisso como diante do apelo de uma nova conquista. Mas é o amor de sexo para sexo que se revela mais nitidamente como um desejo de posse: aquele que ama quer ser possuidor exclusivo da pessoa que deseja, quer ter um poder absoluto tanto sobre a sua alma como sobre o seu corpo, ser amado unicamente, instalar-se e reinar na outra alma como o mais alto e o mais desejável.”
Sem ter mais o que discursar a respeito, hasteio a minha bandeira: A Bandeira Negra, anarquista, aquela cuja representação ostenta o livre pensar, a opinião singular individual, e a cusparada a cruzes ou grupos corrompidos e sem rumo algum.FONTE: DA SILVA, Paulo Neves. Citações e Pensamentos de Nietzsche. Editora, Leya.
11 de dezembro de 2019
Desde os primórdios da humanidade; dos nômades do Período Paleolítico até os dias atuais, indivíduos criam organizações que, invariavelmente, tendem a inevitável entropia (desordem) e decadência.
Hipoteticamente, tais indivíduos integram grupos(facções), cuja finalidade reside na defesa de alguma causa comum a eles; geralmente, as exigências dos integrantes manifestam-se na forma de liberdade e igualdade, quase sempre, em virtude das naturais discrepâncias que as inúmeras organizações existentes possuem entre si.
Decorrentes da essência do homem, corrupta e egoísta, o proposito inicial que deu origem a tais organizações declina com o tempo; a partir desse ponto, os interesses do grupo resumem-se a manutenção do mesmo, independente dos meios que são utilizados para isso, além de servir para mesquinharias individuais dos seus membros; esse processo decadente é análogo a uma célula cancerígena, que outrora possuía uma finalidade útil e após sofrer mutação, luta com unhas e dentes para sua própria sobrevivência, mesmo que para isto destrua tudo a sua volta.
Assim como facções religiosas, políticas, étnicas etc., sofrem da mesma deformação: lutam para que a entidade sobreviva, distorcida ao ponto de sucumbir às trevas o ideal inicialmente proposto.
É fato que a grande maioria destes integrantes, ou melhor, rebanhos humanos são manipulados, como resultado de suas ignorâncias, por líderes, que sim possuem opinião própria, no entanto são desprovidos de escrúpulos, e atingem o status de mártires, mestres e afins.
Como exemplo, não há nada mais covarde e repugnante, do que aqueles que continuam hasteando e militando pela bandeira de facções políticas de direita ou esquerda.
São, na verdade, inúmeros parasitas!
Sem ter mais o que discursar a respeito, hasteio a minha bandeira: A Bandeira Negra, anarquista, aquela cuja representação ostenta o livre pensar, a opinião singular individual, e a cusparada a cruzes ou grupos corrompidos e sem rumo algum.
Viva a Anarquia!
Viva o Pensamento Anarquista!
Viva a Juventude Libertária!
07 de novembro de 2019
Há tempos você, meu grande amor, partiu...
Embora haja ocorrido diversas circunstâncias com as quais nossa relação se desgastou e nos separou, nunca deixaste de ser minha musa inspiradora....
...Contudo, sei que amarei alguém novamente, mas nunca com a mesma intensidade que senti por ti.
Portanto, deixo-lhe, no pequeno verso abaixo uma humilde descrição do que, a mim, significou nossa história de amor:
“Você era tão jovem, e eu era tão livre...
..., mas você foi a única...
..., a única que me mostrou tantas coisas que eu nunca soube ou vi.”
Samuel
05 de novembro de 2019
A física clássica nos deleitou com explicações sólidas a respeito dos fenômenos da natureza.
Dessa forma, seus grandes estudiosos contribuíram com seus legados através da dinâmica newtoniana, einsteiniana e quântica, proporcionando a todos nós, postulados bem definidos dos Sistemas Dinâmicos Estáveis.
Portanto, tais teorias foram refutadas com base em postulações e observações dos Sistemas Isolados de Equilíbrio.
No entanto, os Sistemas Dinâmicos Estáveis devem estar isolados para, assim, perpetuarem o equilíbrio.
De modo que, a manutenção da energia total do sistema depende da não interação deste referencial com outros.
Não obstante, é possível, desde a referência clássica, definir com precisão o passado e o futuro, tornando esse sistema reversível no tempo e, portanto, em equilíbrio.
Em contrapartida, a Teoria do Caos nos diz que um Sistema Dinâmico Instável, sem equilíbrio naturalmente, sofre, invariavelmente, entropia. Isto é, tende à desorganização, o que faz destes sistemas, que sim interagem com outros, perderem informação em relação a uma seta temporal.
Ora, os Sistemas Caóticos não conservam sua energia total, afinal perdem ou adquirem energia através de suas interações com outros sistemas, impossibilitando assim, a manutenção do equilíbrio.
Deste modo, a informação a respeito dos produtos iniciais dos Sistemas Caóticos é perdida, e as previsões sobre o passado e o futuro serão somente adquiridas através de postulações de natureza estatística.
Contudo, como poderemos sustentar a busca da Teoria do Caos a um hipotético equilíbrio retroativo e auto organizado?
Até aqui, estiveram comigo Newton, Einstein e Prigogine; contudo devo, daqui adiante, seguir só, na insignificância que faz do meu conhecimento do que foi exposto acima, estar encerrado.
Assim sendo, farei diferente.
Na parte II deste ensaio, discursarei a respeito da necessidade do desequilíbrio para, então, haver interação. Para isso, utilizarei da forma como concebo a realidade.
Dessa vez, a Escuridão estará comigo! Oh! Adorável companheira!
03 de novembro de 2019
“É da agonia que virá meu triunfo.”
O ateísmo diz:
-Não há deus.
O niilismo diz:
-Não há sentido à vida humana.
O Imperativo Categórico diz:
-Os meios justificam os fins.
Seriam, estas três características, citadas acima, a essência da interpretação que faço da realidade?
Sim! Não há dúvidas, assim vejo o mundo e, consequentemente, sofro da agonia resultante do conflito que tais características apresentam entre si.
É fato que deus não existe, no entanto, para mim, o ateísmo teria mais sentido se Ele existisse, afinal, que diferença faz. Se deus estivesse entre nós, abriria mão de suas oferendas, não as necessito; continuaria, da mesma forma ateu.
É também, uma premissa verdadeira, a inexistência de razão ou sentido à vida humana, ou, de qualquer outro ser vivo; na verdade, a Natureza foi, é, e, sempre será indiferente às entidades vivas. De modo que, meu niilismo parte do pressuposto que me canso, quase sempre temporariamente, das pessoas; sinto-me, verdadeiramente confortável, quando estou a sós, na presença da minha razão, oh! Adorável guardiã!
Em contrapartida, sinto a agonia ontológica de acreditar numa espécie de Imperativo Categórico Kantiano, não necessariamente moral, mas sim, algo parecido a uma “Conspiração Cósmica”, cujos fins são feitos através dos meios e, possibilitam a colheita dos frutos que, outrora foram plantados; de forma análoga, faça o bem e, obtenha seus respectivos resultados.
Sem mais ter o que discursar sobre este assunto concluo:
Sou ateu de fato, absoluto; atinjo o niilismo numa faceta relativa, não creio no homem, tampouco no sentido ou razão de sua existência, entretanto, o Imperativo Categórico, do qual sou crente, impossibilita minha descrença absoluta, e, minha agonia, surge do fato de eu sentir a liberdade das minhas escolhas
01 de novembro de 2019
Ainda hoje faço a pergunta:
- Onde está tudo aquilo a respeito da vida? A virtuosa!?
Tornei-me um cético à medida que acumulei fracassos na vida, e, acreditem, foram muitos.
Mais do que isso, fracassei ao ponto de desenvolver descrença em quase tudo.
São também contribuições deles, dos meus fracassos, os cabelos brancos, precoces em demasia, que hoje predominam sobre minha preocupada cabeça.
Aliás, jamais desfrutei dos poucos êxitos que tive da mesma forma que assim os contemplei antes de atingi-los; de modo que, foram-me geradas frustrações cujas indiferenças resultantes me forçaram a abandonar quase todos eles, os meus sonhos.
É verdade que há muito sou atraído pela libertinagem, de cuja vida incerta impossibilitou que meus anseios da adolescência, tais como mulheres que desejei, ou minha vida acadêmica entre outros, hajam-se concretizado; tornaram-se, na verdade, pó, assim como se tornam pó castelos de areia aos ventos.
Assim é....
Igualmente, fui advertido sobre minhas escolhas, e, mesmo assim, fiz do meu jeito, fato do qual imputa a mim mesmo o dolo pelo desperdício que fiz dela, a minha vida.
Colecionei, de acordo com o que expus acima, feridas que não mais cicatrizam e, são, pois, circunstancias dessas ulceras a razão pela q ual busco freneticamente adquirir conhecimento, cuja finalidade é atenuar, mesmo que infimamente, o sofrimento que a mim é imposto por elas, as tais feridas.
Confesso que o conhecimento não me fez uma pessoa melhor, longe disso.
No entanto, ele (o conhecimento) possibilitou que eu refine minha concepção do mundo ao meu redor através duma poderosa critica singular e analítica.
Ademais, atribuo ao niilismo (descrença absoluta) a bela, austera e fria interpretação que tenho da realidade; é por meio dele (o niilismo) que, afasto-me cada vez mais das pessoas, e, por outro lado, aproximo-me cada vez mais dos cachorros, de pequeno porte se assim for possível.
Sem mais o que dizer concluo ciente que, em poucos anos, a natureza esquecerá de quem algum dia fui...
...que importa...
...para o inferno qualquer delirante sentido que qualquer desprezível convicto possa esperar para a existência...!!!
31 de outubro de 2019
Existe ato mais egoísta do que esperar algo da vida, ou das outras pessoas?
Não seria esta atitude, a de colocar-se forçosamente numa posição dentro do mundo, a manifestação do desespero humano, o grito de socorro daqueles que fogem, desesperadamente, da rejeição, …da verdade…???
Em vista disso, o que esperar da vida? Quais seriam as metas corretas para viver uma vida virtuosa (plena)? Quais seriam os passos necessários para atingir o sucesso, …, o êxito, …, a felicidade…???
Tratando-se da autocritica, através da qual cada indivíduo faz uma análise de si mesmo e, julga a medida exata dos seus logros durante a vida, podendo dizer se atingiu o sucesso, o êxito ou a felicidade e, invariavelmente outorga a sentença da qual apenas ele, o sujeito que julga a si próprio, pode escutar:
- Não, oh não! Não sinto o sucesso, …, a felicidade…
Embora soe como fracasso, é provável que cada ser escute a mesma voz, aquela que traduz a natureza humana, que definitivamente não possui o gene responsável pela plenitude, pela realização, pela sinceridade.
É lastimável existir pessoas que se ocultam atrás de personagens tais como: os light, os vegetarianos, os místicos, os de alto-astral; a ausência de vícios que um indivíduo, desesperadamente, tenta transmitir, retrata o quão difícil é para ele estar consigo próprio, não admitindo a sua natureza.
É através de suas próprias doenças e misérias que um sujeito atinge a sabedoria necessária para conhecer a si próprio, e quiçá, aos outros…; são meus vícios, oh louvados sejam todos eles, os meios dos quais utilizo para atenuar, uma fração que seja, das minhas angustias, do meu desespero, afinal quando enxergo minhas imperfeiçoes, coloco-me em pé de igualdade com os outros…
…e, sem ter mais o que discursar a respeito deste assunto, concluo:
-O único sentido que vejo à vida é a possibilidade de acumular conhecimento e cuspi-lo até o inerente fim.
30 de outubro de 2019
Os homens virtuosos (corajosos) são perseguidos e acusados de hereges pelo fato de criarem suas próprias virtudes através da solidão, através das suas singulares formas de pensar cuja síntese, constrói as suas particulares opiniões.
Esse caminho, o da solidão, proporciona como recompensa, o virtuosismo. Contudo, ele é tortuoso, trilhado com passos torpes, assim como no andar de um bêbado.
A busca pela solidão resulta da agonia daqueles que pensam em demasia, e, dialogam demais consigo próprio; eles sabem que suas agonias causaram feridas, que se transformaram em úlceras das quais carregarão consigo até o dia da verdade.
É fato que, aqueles que buscam a virtude na trilha da solidão, estão sujeitos a se perderem facilmente, entretanto é esse o desafio àqueles que almejam o “ser livre”, a anarquia vivida na sua plenitude.
De qualquer modo a tentativa fracassada é tão virtuosa quanto o êxito.
Não há dúvidas que a escuridão, é a companheira daqueles solitários cuja meta é a virtude. A escuridão, a velha amiga, é portadora da verdade fria, elegante e austera! Oh! Adorável companheira!
Muitas vezes são as trevas que propiciam o mais belo pensamento puro; em contrapartida, muitas pessoas ao redor, penduram-se por muito tempo nos seus ramos; algumas delas, lamentavelmente vivem demais.
Sem mais o que dizer a respeito, rogo:
– Que o meu caminho, solitário e tortuoso, faça com que, eu compreenda, mesmo que infimamente, a realidade, da qual temporariamente, farei parte.
Amém.
23 de outubro de 2019
Não foram poucas as vezes que, a Einstein, perguntaram se ele acreditava em deus ou se ele era religioso.
Quase sempre mal compreendido, ele respondia, grosso modo, às duas perguntas da seguinte forma:
-Sim, acredito, mas no deus de Espinosa (filósofo holandês).
-Em relação à religião, eu diria que sou um profundo devoto da intuição cientifica; portanto sou um religioso que acredita nas equações que regem as leis da natureza.
A confusão resultante das duas afirmações de Einstein, citadas acima, são fruto do paradigma com o qual Einstein concebe deus e religião.
Seu deus, assim como o de Espinosa é a natureza em si, com suas leis esclarecidas através das belas e austeras equações. Isto é, para eles, assim como para mim, não existe um deus consciente que criou tudo ao nosso redor e intervém nas ações humanas; e mais, muito mais do que isso, para a natureza (deus), é indiferente a existência ou não de seres humanos.
Em relação à religião, Einstein se considerava como tal, pois era um devoto convicto de que somente a intuição humana possibilita a descoberta dos segredos de “deus” que são estabelecidos em teorias positivistas compostas por equações matemáticas que progressivamente são refutadas pelas observações da realidade que experimentamos.
Contudo, para ele (Einstein), a simples composição duma teoria física originada pela intuição, e com suas equações em perfeita harmonia, bastava para que o físico com sua língua para fora, a considerasse correta.
Einstein estava tão seguro de sua intuição que a equação que se encontra na figura acima e simplesmente mudou completamente a forma como vemos o Universo, foi concebida por ele na sua Teoria da Relatividade Geral, em 1916.
No entanto, a primeira observação cientifica que deu crédito a ela como correta, foi feita em 1919, na cidade de Sobral no Ceará, através dum breve eclipse estelar.
Dias depois uma secretária correu eufórica pelos corredores da Universidade de Berlim até o escritório de Einstein para dar-lhe as boas novas, mas ele não expressou grande euforia pela novidade. Confusa, a mulher pergunta ao grande cientista:
- O você teria pensado se sua teoria tivesse sido desmentida?
E Einstein respondeu:
- Então deus estaria errado e minha teoria correta!
É disso que trata a verdadeira e única forma religiosa de se conceber o Todo ao nosso redor...
15 de outubro de 2019
A vida é realmente curiosa...
...afinal trânsito dias difíceis:
- A Lei, através dos "justos" quer que eu seja preso.
- Luto exaustivamente para conviver com minha filha, no entanto, ainda não obtive êxito.
- Passei boa parte da minha vida convivendo com inúmeros parasitas dos quais tive o desprazer de conhecer.
Contudo, não reclamo mais da vida que levei, pois colecionei consequências que são frutos dos meus atos.
Paguei e sigo pagando pelo mau, fato que reconheço como verdadeiro.
É equivalente à metáfora deu uma simples e bela equação, com suas proporções de sua esquerda e direita em perfeita harmonia!
Que importa!
Se a vida é uma longa e amarga preparação para a morte.
14 de setembro de 2019
Não me restam dúvidas a respeito do sofrimento que sentiriam aqueles que, cruelmente, fossem submetidos à vida eterna. Sinceramente, não poderia traduzir através das palavras semelhante agonia.
De fato, a maior consolação que existe na finitude é a morte propriamente dita, e, uma boa dose do esquecimento temporal que ela trará.
Contudo, sinto-me frio em demasia quando deixo de pensar naqueles já não estão, sobretudo quando esqueço, mesmo que temporariamente, dos que foram e ainda são importantes para mim.
É por isso que faço aqui homenagens tardias a você, Antonio Capelozzi, meu querido avô.
Seu legado, é para mim, traduzido como aquele que dedicou a sua vida ao trabalho, ao bem-estar dos seus filhos e à formação acadêmica de excelência dos mesmos.
Sabemos bem que os espinhos do destino não conspiraram para que a vida lhe retribua na mesma medida os seus esforços; ao invés disso, ela, a vida, pareceu-lhe injusta, como de fato foi e é.
Em relação ao que aqui escrevo, apenas dou coesão e, quem sabe, coerência às conjecturas fonéticas que de forma alguma possuem o mesmo impacto dos seus feitos em vida, meu avô.
Os fonemas na verdade, são para mim, um breve alivio à culpa que sinto por não valorizar como deveria os momentos dos quais tive a oportunidade de estar com ti enquanto ainda estavas.
De qualquer modo, não se preocupe, afinal agora é a hora do seu merecido descanso, e, cabe a mim, seu neto, a responsabilidade pela sua eternidade, de uma forma ou outra.
Portanto, construo sua eternização através dos seus ensinamentos cuja manifestação se faz mediante as virtudes que creio possuir; e mais, muito mais do que isso, sua eternização já se encontra num novo hospedeiro, minha filhinha, sua bisneta, a qual carrega consigo partes do seu material genético, e, que por sua vez, fará o mesmo, dando ao seu nome, nosso nome, a longevidade que merece...
Obrigado por tudo!
30 de agosto de 2019
“Não existe um homem a quem não tenha acontecido mais do que uma vez desejar não ter de viver o dia seguinte.” Heródoto
Arthur Schopenhauer (O Mundo como Vontade e Representação) costumava dizer que o caráter de um homem é definido pelas suas vontades e os meios pelos quais utiliza para atingi-las .
Tais vontades possuem inúmeras facetas, que vão das mais triviais, costumeiras, ambiciosas, perigosas até as mais cruéis.
Contudo, existe um tipo de vontade que trata especificamente da desesperança;e ela possui dois caminhos um tanto distintos.
No primeiro, a vontade se manifesta no ato de deixar de existir (morrer), quase sempre motivada pela dor, desespero e incapacidade de levantar a cada novo dia para seguir ao menos respirando. Evidentemente a vontade, nesse caso, é alcançada através da morte que na maioria das vezes de consuma com o suicídio.
Em contra partida, existe outro tipo de vontade, também motivada pela desesperança, aliás da qual sou adepto. É aquela necessidade de estar o mais próximo possível dela, a morte. Seria como um parasuicidio, cujos riscos sofridos através da realização dessa vontade fazem com que se visualize a morte materializada, que sorri com malicia.
Sou completamente atraído pelas noites frias e escuras nas ruas, que sempre possuem a possibilidade de deparar-se com uma bala que está à minha espera.
No entanto, sou uma daquelas ovelhas que se perderam por aí, não há ninguém acima de mim, e dessa forma desconfio que a natureza me pune com um condenação brutal: viver eternamente.
O tempo, é para mim, uma mera ilusão, portanto se vivo o agora escrevendo estas tortas linhas, em nada se diferenciaria se aqui não mais estivesse, pois não poderia contemplar a respeito, estaria morto.
Que importa! Já estou perdido há muito, ou melhor, nunca deixei de estar.
Sou o que sou, e a vontade da desesperança, brilhantemente discursada por Schopenhauer inunda os meus pensamentos.
Não se trata de julgar qual é a vontade de cada um, mas sim quais são os meios que o indivíduo utiliza para saboreá-la.
Existiria alguém capaz de julgar a vontade do outro?
Não poderia encerrar, é claro, sem antes citar Kafka:
“Esperança há muita por ai, mas não para nós.”
27 de agosto de 2019
Chaplin recorda um jantar, em 1926, na sua casa da Califórnia em que estavam presentes Einstein, a Sra. Einstein (sua segunda mulher) e dois amigos. Durante o jantar a Sra. Einstein concebeu a teoria da relatividade.
Ela relatou-lhe:
O Doutor [Einstein] desceu em roupão para o pequeno-almoço como de costume mas mal lhe tocou. Pensei que haveria algo de errado e perguntei-lhe o que é que o preocupava. Querida, disse ele, tenho uma ideia maravilhosa. E, após ter bebido o café, foi para o piano e começou a tocar! Interrompeu e repetiu, tenho uma ideia maravilhosa. Ao que eu respondi: Então, por amor de deus, diz-me o que é, não me mantenha na expectativa, ao que ele replicou: É difícil, tenho ainda de a trabalhar.
A Sra. Einstein disse a Chaplin que Einstein continuou a tocar o piano durante cerca de meia hora e então subiu as escadas para o escritório dizendo-lhe que não queria ser incomodado e lá permaneceu durante duas semanas.
Todos os dias lhe mandava para cima refeições e ao fim da tarde andava um pouco para se exercitar e voltava para o seu trabalho.
Um dia, veio para baixo com um aspecto muito pálido. Aqui está, disse-me em tom fatigado pondo duas folhas de papel em cima da mesa. Aquilo era a sua teoria da relatividade.
FONTE: O Sonho de Einstein – Barry Parker
E foi assim , que ele (Einstein) desenvolveu o maior êxito intelectual de todos os tempos...
26 de agosto de 2019
É fato que todos nós sabemos a verdade, mas quase sempre, preferimos as mentiras.
Conversando com os antigos, deparei-me com belas e austeras reflexões sobre ela, a morte, cuja veracidade ou falácia, a mim, pouco importa; portanto, seguem adiante algumas delas:
“Os escolásticos ensinaram que a eternidade não é uma sucessão do tempo sem princípio ou fim, mas que existe agora: ou seja,
vivemos agora o mesmo que outrora Adão vivera: isto é, não há distinção entre agora e outrora.”
Schopenhauer
“Ninguém está verdadeiramente convencido de que a sua própria morte esteja assegurada, senão não poderia haver grande diferença entre a
sua sorte e a do criminoso que acaba de ser condenado; com efeito, cada um reconhece bem, e em teoria, que sua morte é certa, mas esta
verdade é como muitas outras que se julgam inaplicáveis na pratica: colocam-se de lado, não contam entre as ideias vivas, atuantes.”
Schopenhauer
“Quando um homem morre, a sua visão confunde-se com o sol, o seu odor com a terra, o seu gosto com a agua, a sua alma com o ar,
a sua palavra com o fogo etc..”
Vedas
“Há uma cerimônia feita pela qual o moribundo leva a um dos seus filhos os seus sentidos e todas as suas faculdades: o todo deve reviver nesse filho.”
Vedas
“O que tememos na morte não é a dor: primeiro é demasiado evidente que o domínio da dor está para aquém da morte; em seguida, muitas
vezes é para fugir da dor que as pessoas se refugiam na morte: o caso não é mais raro do que o contrário, aquele em que o homem
suporta os sofrimentos mais atrozes enquanto a morte está lá, à mão, rápida e fácil e ele sofre precisamente para afastá-la nem que seja por um momento.”
Schopenhauer
“Aqui será minha morada; aqui farei homens,
À minha imagem,
Raça que se parece comigo;
Fá-lo-ei para o sofrimento, para as lágrimas,
E fá-lo-ei a não te respeitarem,
Como eu!”
O deus do povo escolhido; o punitivo!
“Deixai toda a esperança, ó vós que entrais.”
Os dizeres da porta do inferno, segundo Dante Alighieri
08 de agosto de 2019
Olá meu querido pai; não poderia eu, de forma alguma, não desejar-lhe um feliz dia dos pais.
Quero que saiba que todos, eu disse todos os dias, você, de uma forma ou outra, está comigo.
Afinal, os laços que nos unem sempre serão maiores e mais fortes do que aqueles que nos afastariam.
Felizmente, você e eu não nascemos com o dom da fé, portanto o tempo é pra nós somente uma sucessão ordenada de eventos que sucumbe diante da grandeza da natureza.
Contudo, nossa tradição familiar eterniza nossas breves existências transmitimo-las de pai para filho. E você já fez isso com excelência.
Agora é a minha vez, pois não desistirei jamais de perpetuar a sua figura, relatando à milha filha Victória, sua neta, o grande homem que você foi.
Nesse exato momento que escrevo essas torpes linhas você descansa merecidamente.
Por outro lado, ainda não sou digno da dadiva da finitude, pois todavia, tenho pendencias a serem resolvidas.
Sem mais o que dizer, repito:
- Você foi e sempre será minha maior inspiração!
Do seu filho Samuel.
Olá amigos, inimigos e aspirantes a ambos das redes sociais...
Aqui estou novamente, reencontrando-me com a justiça. Aquela mesma cujo rigor é imposto através daqueles que se intitulam como os justos àqueles como eu, os ditos infratores do dogma penal.
Contudo, ela (a Justiça), na sua representação feminina dos antigos gregos, mostrou-me sua face mais bela, e proferiu a absolvição daquilo que não fiz.
Posso, portanto, seguir a trilhado meu caminho, cujos passos incertos me obrigam a sugerir a todos que não me sigam, afinal estou perdido há muito...
A meus amigos os saúdo, digo-lhes que continuo estando...
....e a meus inimigos, inúmeros parasitas dos quais tive o desprazer de conhecer, novamente faço a pergunta:
- Quem morrerá primeiro?
A simetria ou as leis conservativas da natureza tratam, basicamente, de alguma quantidade mensurável dentro dum sistema que se mantem constante; isto é, os produtos iniciais de determinado sistema de eventos, por mais que sofram mudanças possuem suas quantidades imutáveis nos processos finais dos mesmos. Dessa forma, não há perda de informação durante o ciclo.
A terceira lei de Newton é um perfeito exemplo da física clássica onde uma força que age com uma ação, sofre em contrapartida uma reação de igual intensidade, respeitando as leis conservativas e simétricas da natureza. Os processos energéticos por mais que se transformem, constantemente em diferentes formas de energia possuem suas quantidades iniciais e finais constantes; são, portanto, interações simétricas.
Obviamente sou adepto à elegância das leis clássicas da natureza, cujas ações humanas não são exceção e, portanto, respeitam as mesmas leis simétricas.
Desse modo, qualquer ação humana terá como composição simétrica uma reação que se origina na realidade ao redor do ator que sofrerá, invariavelmente, o peso das leis simétricas. Assim, pois, uma ação negativa terá como resposta uma reação negativa.
Enfatizo, desde já, que este ensaio somente faz sentido sobre a ótica ateísta e libertaria.
Tratei até aqui, da forma como vejo o mundo: simétrico, cujas leis físicas são as mesmas para qualquer sistema observado. Daqui adiante tratarei do conceito de vingança; e mais, muito mais do que isso, tentarei demonstrar que ela (a vingança) é diretamente relacionada às leis simétricas e ao inevitável processo de causa e efeito.
E, para isso, farei uso do fatídico episodio do caso do ex-prefeito de Santo André – SP; mais precisamente, falarei de meu pai, que sucumbiu nesse caso em razão de haver sido o médico legista que fez a necropsia de Daniel e atestando, portanto, tortura seguida de homicídio.
Deixo claro, desde já que não busco justiça, mas sim vingança. Do mesmo modo que Golda Meir, uma guerreira anarquista, que quando Primeira-ministra de Israel, vingou os atletas israelenses mortos na lamentável olimpíada de Munique, em 1972. Meir caçou, um a um, os onze lideres covardes do grupo terrorista Setembro Vermelho, que mataram inocentes em nome de deus.
Meu pai, como qualquer um, tinha defeitos; não obstante, tinha também qualidades; e, no caso Celso Daniel, especificamente, foi corajoso o bastante para manter a sua versão técnica de tortura, mesmo sofrendo pressão das cúpulas dos poderes legislativo e executivo do estado de São Paulo e da União.
Ele sabia que era seu fim, no entanto, foi incapaz de trair a si próprio!
Dessa forma, aqui estou, sedento por vingar meu querido pai; e esperançoso para isso, afinal outro parasita, Antonio Palocci, provavelmente trará novas informações sobre o caso Celso Daniel, na sua já deferida delação premiada.
Meu alvo são dois desprezíveis parasitas, afinal Lula e Dirceu já estão pagando; o primeiro é o ex-deputado federal pelo PT Luiz Eduardo Greenhalgh, que além de estar envolvido na morte de Daniel, esteve presente durante a necropsia do mesmo, atrapalhando o trabalho do legista, no caso era meu pai, que por sua vez foi obrigado a expulsar Greenhalgh do necrotério a socos e pontapés. O ex-deputado perseguiu, desde então meu pai.
Por fim, o último, é o editor chefe da revista Carta Capital, que escreveu um livro inteiro defendendo a tese que meu pai era o protagonista duma conspiração, que aos olhos do PT, era uma perseguição política; um disparate!
Sou a favor da liberdade de imprensa, a honesta, afinal sou anarquista.
A simetria relaciona-se aqui através dum conhecido ditado, análogo à explicação que fiz acima sobres as leis simétricas...
...AQUI SE FAZ, AQUI SE PAGA!
Sem mais o que dizer, não descansarei e enquanto viver farei o que for possível para acabar com a raça de vocês, seus parasitas imundos! É uma dívida que tenho com meu querido pai, que agora descansa.
É disso que trata a minha vingança simétrica...
Samuel Delmonte
Olá a todos.
Desejo-lhes, primeiramente, um bom ano; que muitas das suas aspirações se concretizem.
Comecei 2018 cometendo um erro; pago atualmente, portanto, pelas consequências de tal equívoco.
0 Não é aqui relevante determinar se, de fato, errei ou não; depende, é claro, do ponto de referência que possa dar sentido às circunstancias, se é que isso é possível.
Logo, há uma série de fatores que podem ser utilizados para referenciar hipotéticas situações, tais como: a ética, o conjunto de preceitos (dogmas) morais grupais, a lei dos justos (código penal), dentre outros.
Não existem, ao meu ver, leis morais universais; são todas elas criações do homem para controlar e oprimir; de modo que não é possível adequar certa situação à uma única visão, que por sua vez é desprovida de argumentos determinísticos, mas sim circunstanciais. Assim sendo, há muitas possibilidades de interpretação ao ato em si, e, cabe logicamente fazer uso de referências para tais interpretações.
Ademais, o dolo ou a imputabilidade que os fatores citados acima possam caracterizar, não querem, a mim, dizer nada.
Contudo, existe uma estranha voz que perturba e faz com que eu pergunte a mim mesmo:
-Estaria eu disposto a passar por cima de tudo e de todos para me ver livre?!
Tal voz, cujas aparições também assombraram a Papillon (Henri Charriére) em muitos momentos dos seus terríveis sete anos de solitária na prisão da Guiana Francesa, materializa-se, de fato, como a Consciência, a própria consciência.
Embora pareça loucura, o diálogo com ela, a consciência, se faz nos instantes mais desprezíveis da monotonia e da sobriedade.
Esse encontro traduz a mais fria e austera verdade, afinal minha consciência, análoga a um júri, outorga a sentença dum dos piores crimes que um ser humano pode cometer:
O desperdício que fiz dela, a minha vida...
...crime do qual sou culpado. Ó sim! Culpado!
Não encontro meios para fugir dessa realidade; ela, na verdade, persegue-me até o fim.
No entanto, há males que vem para bem e estou em processo de retomada; penso que poderia ser pior, e com certeza poderia.
Alivio-me, portanto, em duas qualidades que acredito possuir: a resiliência e a saúde.
Acredito, não sei ao certo como, na evolução, o que certamente fará com que eu seja uma pessoa melhor.
Sei que falta muita coisa na minha vida e, assim como lhes desejei, aspiro também atingir muitos objetivos pessoais.
Que assim seja...!!!
“...Minhas crianças serão testemunhas de um apocalipse lento e cruel, assombrado por fanáticos religiosos, políticos psicopatas e uma polícia assassina quer, em vez de proteger, massacra a população em nome do sistema.” Viva la vida tosca – João Gordo
Não poderia deixar de assinar embaixo e concordar com o conteúdo do trecho acima, que extrai da autobiografia de João Gordo. Aliás, excelente obra, escrita com uma coesão da linguagem coloquial brilhante; ao ler o livro parece até que ele (João Gordo) está presente, relatando numa conversa bem informal suas histórias.
Gordo é para mim um punk de verdade, afinal e, além de ser meu vizinho, expressa nitidamente o fundamento do anarquismo, que se manifesta, sobretudo, no livre pensar, ou melhor, na arte de pensar com a própria cabeça.
Esse pensamento anarquista, inevitavelmente, transforma as opiniões de seus adeptos em sucessivas contradições que vão, com o passar do tempo, sendo desconstruídas, refinadas e reformuladas.
O homem contraditório se permite pensar, perturba-se com suas malditas convicções e as abandona uma a uma. O processo de deixar de acreditar alimenta o ceticismo que, por sua vez, constrói a dúvida a respeito de quase tudo, elimina o fanatismo e possibilita o desenvolvimento da tolerância, atributo que atualmente encontra-se em extinção.
Recomendo, portanto, a todos a autobiografia de João Gordo – Viva la vida tosca -, livro que apresenta mais uma visão anarquista desse mundo.
Louvado seja o João Gordo....
Louvado seja o pensamento anarquista...
Louvada seja a juventude libertaria...!!!
Dale dale sou São Paulo até morrer!
Dale dale meu São Paulo amo você.
Dale dale sou São Paulo até morrer!
É por você meu tricolor que estou aqui...
Tremendo a bancada do Morumbi...
O teu nome com alegria eu vou gritar.
És um vicio que jamais quero curar!
Sou torcedor, com muito amor do Soberano Tricolor...
Se vai jogar, eu vou te ver... Tu és orgulho e meu viver.
Dale dale meu São Paulo amo você.
Dale dale sou São Paulo até morrer!
Dale dale meu São Paulo amo você.
Dale dale sou São Paulo até morrer!
É por você meu tricolor que estou aqui...
Tremendo a bancada do Morumbi...
O teu nome com alegria eu vou gritar.
És um vicio que jamais quero curar!
Sou torcedor, com muito amor do Soberano Tricolor...
FONTE: https://www.youtube.com/watch?v=h9IEqPepkw0&feature=share
Não poderia eu aqui deixar de prestar minhas homenagens a você Gegê, o Gegê do Mangue, ou melhor, Rogério, que foi mais um daqueles moleques que cresceram no fim dos anos oitenta e inicio dos noventa no bairro da Vila Madalena.
Naquela época nos juntávamos entre as ruas Girassol, Rodésia e Fidalga para empinar pipas e jogar futebol sobre o asfalto das ruas; vivíamos esfolados.
Cresci com os meninos do mangue, e vi um a um viverem rápido demais e morrerem jovens demais.
Assim como eles fiz minhas escolhas; embora não tão radicais, elas (escolhas) tornaram minha juventude conturbada e fizeram com que muitos daqueles que se intitulam como os justos me apontassem como um marginal.
A opinião desses desprezíveis indivíduos não querem, a mim, dizer nada. Prometi a mim mesmo que estarei presente na maior parte dos enterros desses inúteis, sóbrio, sereno e respeitoso como devem ser os rituais fúnebres.
Mas, sem desviar do assunto, trato nessas linhas das lembranças que tenho dele, o Gegê, que também fez suas escolhas, sendo que muitas delas lhes cobraram um preço alto. Dentre suas escolhas na vida, sofreu uma condenação de dezessete anos, passando boa parte desse tempo no RDD (Regime disciplinar diferenciado).
No cárcere tornou-se membro duma irmandade, que a priori, pregava a pacífica convivência entre os presos do sistema penal paulista.
Gegê fez o que era necessário para manter tal ideal vivo. Não é aqui relevante determinar se suas condutas aderiam ou não a dogmas morais, que na prática, fazem sentido apenas em liberdade. Na prisão, infelizmente, decisões extremas são tomadas para não desmoralizar àqueles que as necessitam impor. Não me sinto apto a julgar tais procedimentos.
O que sim afirmo com segurança é que não existem grupos formados por pessoas que lutem por um determinado ideal incondicionalmente; na verdade o ideal em si se dilui com o tempo e os membros de qualquer organização passam a distorcer o propósito de suas existências através de interesses conflitantes e mesquinharias individuais.
Gegê foi traído e morto barbaramente
Rogo para que aqueles que dele gostavam sofram o menos possível.
E, desde já abandono o lema – Paz, justiça e liberdade -, que não passam de palavras que vagueiam aos ventos, afinal vivemos uma solidão muito maior do que imaginamos.
Sem mais o que dizer:
- Descanse em paz Rogério (Gegê)!
Em A Desordem: a arte de pensar com a própria cabeça, o autor revela, sem pudor, sua opinião a respeito dos assuntos mais polêmicos e controversos da atualidade. Aqui você encontrará 30 ensaios curtos, de fácil leitura, todos com começo, meio e fim, cujos temas abordados incluem religião, política, ciência, cultura, sociedade e muitos outros.
ISBN: 978-65-250-0360-3
Edição: 1ª
Ano da edição: 2021
Data de publicação: 01/04/2021
Número de páginas: 101
Encadernação: Brochura
Peso: 100 gramas
Largura: 14.8 cm
Comprimento: 21 cm
Altura: 2 cm
1. Samuel Delmonte.
Em A Desordem: a arte de pensar com a própria cabeça, o autor revela,
sem pudor, sua opinião a respeito dos assuntos mais polêmicos e controversos da atualidade.
Aqui você encontrará 30 ensaios curtos, de fácil leitura, todos com começo, meio e fim, cujos
temas abordados incluem religião, política, ciência, cultura, sociedade e muitos outros.
O livro é escrito com base em algumas tendências filosóficas tais como o Romantismo, Ceticismo,
Realismo e o Anarquismo Filosófico, que estão longe de ser propostas de organização, ou de um movimento
qualquer; pelo contrário, são eles uma forma de rebelião intelectual, uma resistência ao autoritarismo dos
dogmas e costumes preconcebidos, impostos por uma sociedade decadente, que se arrasta e já não mais sustenta
o seu discurso do politicamente correto.
Esta obra é indicada para aqueles de espírito livre, que pouco a pouco se libertam das garras
da servidão e já não toleram ser submetidos, às cegas, às palavras e dizeres de ninguém, sem antes
refletir e discernir a respeito, para então emitir sua opinião singular sobre o que lhe foi dito.
O autor recomenda o livro também a todos aqueles de opinião e visão de mundo distintas.
Seria uma excelente oportunidade para refutarem ou, quiçá, reformularem suas concepções sobre
a realidade que nos cerca.
Somente quando questionamos as coisas estamos exercendo o ato de
pensar. Aceitar condições impostas sem antes raciocinar o porquê alimenta a ignorância.
❞Nos dias de hoje, apenas nos ateus sobrevive a paixão pelo divino. Nenhum outro se salvará.
❞Estar sozinho é treinarmo-nos para a morte.
❞“Cavalheiros...
..., a vida é curta.
Se vivemos...
...vivemos para pisotear a cabeça dos reis.”
❞Guardemos no mais profundo de nós mesmos uma certeza superior a todas as outras: a vida não tem sentido, não pode tê-lo.
❞O futebol é a coisa mais importante, das coisas menos importantes.
❞...Pois vocês são o povo escolhido pelo senhor, nosso deus; entre todos os povos da terra ele escolheu vocês para serem somente dele.
❞Não há o que temer, a alma é finita e não há vida após a morte.
❞O cristianismo foi, até o momento, a maior desgraça da humanidade, por ter desprezado o Corpo.
❞A natureza não é cruel, apenas implacavelmente indiferente. Esta é uma das l ições mais duras que os humanos têm de aprender .
❞Tenho de proclamar a minha incredulidade. Para mim não há nada de mais elevado que a ideia da inexistência de Deus. O homem inventou Deus para poder viver sem se matar.
PARTE 2
❞Eu vejo o que está certo e aprovo, mas faço o que está errado.
❞Se Deus não existe, então tudo é possível e permitido!?
❞Que lamentável condição do homem! Ter que ser domado pelo medo ao castigo e pela esperança de uma recompensa depois da morte.
❞O importante é a escolha moral. O mal tem que existir junto com o bem, para que a escolha moral possa funcionar. A vida é sustentada pela oposição das entidades morais.
❞Os encantos dessa sublime ciência se revelam apenas àqueles que tem coragem de irem a fundo nela.
❞A primeira lei da natureza é a tolerância – já que temos todos uma porção de erros e fraqueza.
❞O ódio é a vingança do covarde.
❞Parece-me que jamais haverá coragem naquele ou naqueles que idolatram líderes; restará a eles, portanto, covardia.
❞Todo pobre-diabo que não tem nada no mundo do que possa se orgulhar escolhe a nação a que pertence como último recurso para sentir orgulho: desse modo, ele se restabelece, sente-se grato e pronto para defender com unhas e dentes todos os erros e absurdos próprios dessa nação.
❞O cristianismo tornou a crença sem reflexão em uma sabedoria, a hipocrisia humana em conselho divino, a corrupção da lei natural em piedade religiosa, o estudo em loucura, a honra em riqueza, a dignidade em elegância, a prudência na malícia, a traição na sabedoria e a justiça na tirania.
❞“...não acredites nos seus líderes, pois todos eles irão te trair...”
❞.A religião serve para o homem`... ...assim como a viseira serve para o cavalo. Jamais poderá admitir, cristão... ..., que alguém mais inteligente e estudioso que tu, questione tuas crenças... ..., porque sabes que toda a sua vida está apoiada em mentiras incuráveis...
PARTE 3
❞É da agonia que virá meu triunfo.
❞-Sim, acredito, mas no deus de Espinosa (filósofo holandês).
❞Não existe um homem a quem não tenha acontecido mais do que uma vez desejar não ter de viver o dia seguinte.
❞Esperança há muita por ai, mas não para nós.
❞Os escolásticos ensinaram que a eternidade não é uma sucessão do tempo sem princípio ou fim, mas que existe agora: ou seja, vivemos agora o mesmo que outrora Adão vivera: isto é, não há distinção entre agora e outrora.
❞Ninguém está verdadeiramente convencido de que a sua própria morte esteja assegurada, senão não poderia haver grande diferença entre a sua sorte e a do criminoso que acaba de ser condenado; com efeito, cada um reconhece bem, e em teoria, que sua morte é certa, mas esta verdade é como muitas outras que se julgam inaplicáveis na pratica: colocam-se de lado, não contam entre as ideias vivas, atuantes.
❞Há uma cerimônia feita pela qual o moribundo leva a um dos seus filhos os seus sentidos e todas as suas faculdades: o todo deve reviver nesse filho.”
❞Há uma cerimônia feita pela qual o moribundo leva a um dos seus filhos os seus sentidos e todas as suas faculdades: o todo deve reviver nesse filho.”
❞Quando um homem morre, a sua visão confunde-se com o sol, o seu odor com a terra, o seu gosto com a agua, a sua alma com o ar, a sua palavra com o fogo etc..
❞O que tememos na morte não é a dor: primeiro é demasiado evidente que o domínio da dor está para aquém da morte; em seguida, muitas vezes é para fugir da dor que as pessoas se refugiam na morte: o caso não é mais raro do que o contrário, aquele em que o homem suporta os sofrimentos mais atrozes enquanto a morte está lá, à mão, rápida e fácil e ele sofre precisamente para afastá-la nem que seja por um momento.
❞Deixai toda a esperança, ó vós que entrais.
❞...Minhas crianças serão testemunhas de um apocalipse lento e cruel, assombrado por fanáticos religiosos, políticos psicopatas e uma polícia assassina quer, em vez de proteger, massacra a população em nome do sistema.
Go to Text
Go to Text
Go to Text
Phone:
Email: scdelmonte@hotmail.com